| CONTENTS |
This chapter describes the numeric components of the C++ standard library. In particular, it presents the class for complex numbers, the classes for value arrays, and the global numeric functions, which are inherited from the C library.
Two other numeric components in the C++ standard library are described in other parts of this book:
The STL contains some numeric algorithms that are described in Section 9.11.
For all fundamental numeric data types, the implementation-specific aspects of their representation are described by numeric_limits, as described in Section 4.3.
The C++ standard library provides the template class complex<> to operate on complex numbers. Just to remind you: Complex numbers are numbers that have two parts — real and imaginary. The imaginary part has the property that its square is a negative number. In other words, the imaginary part of a complex number is the factor i, which is the square root of minus 1.
The class complex is declared in the header file <complex>:
#include <complex>
In <complex>, the class complex is defined as follows:
namespace std {
template <class T>
class complex;
}
The template parameter T is used as the scalar type of both the real and the imaginary parts of the complex number.
In addition, the C++ standard library provides three specializations for float, double, and long double:
namespace std {
template<> class complex<float>;
template<> class complex<double>;
template<> class complex<long double>;
}
These types are provided to allow certain optimizations and some safer conversions from one complex type to the other.
The following program demonstrates some of the abilities of class complex to create complex numbers, print different representations of complex numbers, and perform some common operations on complex numbers.
// num/complex1.cpp #include <iostream> #include <complex> using namespace std; int main() { /*complex number with real and imaginary parts *-real part: 4.0 *-imaginary part: 3.0 */ complex<double> c1(4.0,3.0); /*create complex number from polar coordinates *-magnitude:5.0 *-phase angle:0.75 */ complex<float> c2(polar(5.0,0.75)); // print complex numbers with real and imaginary parts cout << "c1: " << c1 << endl; cout << "c2: " << c2 << endl; //print complex numbers as polar coordinates cout << "c1: magnitude: " << abs (c1) << " (squared magnitude: " << norm(c1) << ") " << " phase angle: " << arg(c1) << endl; cout << "c2: magnitude: " << abs(c2) << " (squared magnitude: " << norm (c2) << ") " << " phase angle: " << arg(c2) << endl; //print complex conjugates cout << "c1 conjugated: " << conj(c1) << endl; cout << "c2 conjugated: " << conj(c2) << endl; //print result of a computation cout << "4.4 + c1 * 1.8: " << 4.4 + c1 * 1.8 << endl; /*print sum of c1 and c2: *-note: different types */ cout << "c1 + c2: " << c1 + complex<double>(c2.real(),c2.imag()) << endl; // add square root of c1 to c1 and print the result cout << "c1 += sqrt(c1): " << (c1 += sqrt(c1)) << endl; }
The program might have the following output (the exact output depends on the implementation specific properties of the type double):
c1: (4,3) c2: (3.65844,3.40819) c1: magnitude: 5 (squared magnitude: 25) phase angle: 0.643501 c2: magnitude: 5 (squared magnitude: 25) phase angle: 0.75 c1 conjugated: (4,-3) c2 conjugated: (3.65844,-3.40819) 4.4 + c1 * 1.8: (11.6,5.4) c1 + c2: (7.65844,6.40819) c1 += sqrt(c1): (6.12132,3.70711)
A second example contains a loop that reads two complex numbers and processes the first complex number raised to the power of the second complex number:
// num/complex2.cpp #include <iostream> #include <complex> #include <cstdlib> #include <limits> using namespace std; int main() { complex<long double> c1, c2; while (cin.peek() != E0F) { // read first complex number cout << "complex number c1: "; cin >> c1; if (!cin) { cerr << "input error" << endl; return EXIT_FAILURE; } //read second complex number cout << "complex number c2: "; cin >> c2; if (!cin) { cerr << "input error" << endl; return EXIT.FAILURE; } if (c1 == c2) { cout << "c1 and c2 are equal !" << endl; } cout << "c1 raised to the c2: " << pow(c1,c2) << endl << endl; // skip rest of line cin.ignore (numeric_limits<int>::max(),'\n'); } }
Table 12.1 shows some possible input and output of this program.
| c1 | c2 | Output |
|---|---|---|
| 2 | 2 | c1 raised to c2: (4,0) |
| (16) | 0.5 | c1 raised to c2: (4,0) |
| (8,0) | 0.333333333 | c1 raised to c2: (2,0) |
| 0.99 | (5) | c1 raised to c2: (0.95099,0) |
| (0,2) | 2 | c1 raised to c2: (-4,4.89843e-16) |
| (1.7,0.3) | 0 | c1 raised to c2: (1,0) |
| (3,4) | (-4,3) | c1 raised to c2: (4.32424e-05,8.91396e-05) |
| (1.7,0.3) | (4.3,2.8) | c1 raised to c2: (-4.17622,4.86871) |
Note that you can input a complex number by passing only the real part as a single value with or without parentheses or by passing the real and imaginary parts separated by a comma in parentheses.
The template class complex provides the operations described in the following subsections.
Table 12.2 lists the constructors and assignment operations for complex. The constructors provide the ability to pass the initial values of the real and the imaginary parts. If they are not passed, they are initialized by the default constructor of the value type.
The assignment operators are the only way to modify the value of an existing complex number. The computed assignment operators +=, -=, *=, and /= add, subtract, multiply, and divide the value of the second operand to, from, by, and into the real part of the first operand. The imaginary part of both operands is left unchanged.
The auxiliary polar() function provides the ability to create a complex number that is initialized by polar coordinates (magnitude and phase angle in radians):
// create a complex number initialized from polar coordinates
std::complex<double> c2(std::polar(4.2,0.75));
A problem exists when you have an implicit type conversion during the creation. For example, this notation works:
std::complex<float> c2(std::polar(4.2,0.75)); // OK
However, the following notation with the equal sign does not:
std::complex<float> c2 = std::polar(4.2,0.75); // ERROR
| Expression | Effect |
|---|---|
| complex c | Creates a complex number with 0 as the real part and 0 as the imaginary part (0 + 0i) |
| complex c(1.3) | Creates a complex number with 1.3 as the real part and 0 as the imaginary part (1.3 + 0i) |
| complex c(1.3,4.2) | Creates a complex number with 1.3 as the real part and 4.2 as the imaginary part (1.3 + 4.2i) |
| complex c1(c2) | Creates c1 as a copy of c2 |
| polar (4. 2) | Creates a temporary complex number from polar coordinates (4.2 as magnitude rho and 0 as phase angle theta) |
| polar (4. 2, 0.75) | Creates a temporary complex number from polar coordinates (4.2 as magnitude rho and 0.75 as phase angle theta) |
| conj (c) | Creates a temporary complex number that is the conjugated complex number of c (the complex number with the negated imaginary part) |
| c1 = c2 | Assigns the values of c2 to c1 |
| c1 += c2 | Adds the value of c2 to c1 |
| c1 -= c2 | Subtracts the value of c2 from c1 |
| c1 *= c2 | Multiplies the value of c2 by c1 |
| c1 /= c2 | Divides the value of c2 into c1 |
This problem is discussed in the next subsection.
The auxiliary conj() function provides the ability to create a complex number that is initialized by the conjugated complex value of another complex number (a conjugated complex value is the value with a negated imaginary part):
std::complex<double> c1(1.1,5.5);
std::complex<double> c2(std::conj (c1)) ; // initialize with
// complex<double>(1.1,-5.5)
The constructors of the specializations for float, double, and long double are designed in such a way that safe conversions such as complex<float> to complex<double> are allowed to be implicit, but less safe conversions such as complex<long double> to complex<double> must be explicit (see page 542 for the declarations in detail):
std::complex<float> cf; std::complex<double> cd; std::complex<long double> cld; ... std:: complex<double> cd1 = cf; // OK: safe conversion std::complex<double> cd2 = cld; // ERROR: no implicit conversion std::complex<double> cd3(cld); // OK: explicit conversion
In addition, there are no constructors from any other complex type defined. In particular, you can't convert a complex with an integral value type into a complex with value type float, double, or long double. However, you can convert the values by passing the real and imaginary parts as separate arguments:
std::complex<double> cd; std::complex<int> ci; ... std::complex<double> cd4 = ci; // ERROR: no implicit conversion std::complex<double> cd5(ci); // ERROR: no explicit conversion std::complex<double> cd6(ci.real(), ci.imag()); // OK
Unfortunately, the assignment operators allow less safe conversions. They are provided as template functions for all types. So, you can assign any complex type as long as the value types are convertible[1]:
std::complex<double> cd; std::complex<long double> cld; std::complex<int> ci; ... cd = ci; // OK cd = cld; // OK
This problem also relates to polar() and conj(). For example, the following notation works fine:
std::complex<float> c2(std::polar(4.2,0.75)); // OK
But, the notation with the equal sign does not:
std::complex<float> c2 = std::polar(4.2,0.75); // ERROR
The reason for this is that the expression
std::polar(4.2,0.75)
creates a temporary complex<double> and the implicit conversion from complex<double> to complex<float> is not defined.[2]
Table 12.3 shows the different functions provided to access the attributes of complex numbers.
| Expression | Effect |
|---|---|
| c.real() | Returns the value of the real part (as a member function) |
| real(c) | Returns the value of the real part (as a global function) |
| c.imag() | Returns the value of the imaginary part (as a member function) |
| imag(c) | Returns the value of the imaginary part (as a global function) |
| abs(c) | Returns the absolute value of c |
| norm(c) | Returns the squared absolute value of c(c.real()2 + c.imag()2) |
| arg(c) | Returns the angle of the polar
representation of c
|
Note that real() and imag() provide only read access to the real and the imaginary parts. To change only the real part or only the imaginary part you must assign a new complex number. For example, the following statement sets the imaginary part of c to 3.7:
std::complex<double> c; ... c = std::complex<double>(c.real(),3.7);
To compare complex numbers, you can only check for equality (Table 12.4). The operators == and != are defined as global functions so that one of the operands may be a scalar value. If you use a scalar value as the operand it is interpreted as the real part, with the imaginary part having the default value of its type (which is usually 0).
| Expression | Effect |
|---|---|
| c1 == c2 | Returns whether c1 is equal to c2 (c1.real()==c2.real() && c1.imag()==c2. imag()) |
| c == 1.7 | Returns whether c is equal to 1.7 (c.real()==1.7 && c.imag()==0.0) |
| 1.7 == c | Returns whether c is equal to 1.7 (c.real()==1.7 && c.imag()==0.0) |
| c1 != c2 | Returns whether c1 differs from c2 (c1.real()!=c2.real() || c1.imag() !=c2 imag()). |
| c != 1.7 | Returns whether c differs from 1.7 (c.real() !=1.7 || c.imag() !=0.0) |
| 1.7 != c | Returns whether c differs from 1.7 (c.real() !=1.7 || c.imag() !=0.0) |
Other comparison operations, such as operator <, are not defined. Although it is not impossible to define an ordering for complex values, such orderings are neither very intuitive nor very useful. Note, for example, that the magnitude of complex numbers by itself is not a good basis to order complex values because two complex values can be very different and yet have identical magnitude (1 and -1 are two such numbers). An add hoc criterion can be added to create a valid ordering. For example, given two complex values c1 and c2, you could deem c1 < c2 when |c1| < |c2| or, if both magnitudes are equal, when arg(c1) < arg(c2). However, such a criterion invariably has little or no mathematical meaning.[3]
As a consequence, you can't use complex as the element type of an associative container (provided you use no user-defined sorting criterion). This is because associative containers use the function object less<>, which calls operator <, to be able to sort the elements (see Section 5.10.1,).
By implementing a user-defined operator < you could sort complex numbers and use them in associative containers. Note that you should be very careful not to pollute the standard namespace. For example:
template <class T>
bool operator< (const std::complex<T>& c1,
const std::complex<T>& c2)
{
return std::abs(c1)<std::abs(c2) ||
(std::abs(c1)==std::abs(c2) &&
std::arg(c1)<std::arg(c2));
}
Complex numbers provide the four basic arithmetic operations and the negative and positive signs (Table 12.5).
| Expression | Effect |
|---|---|
| c1 + c2 | Returns the sum of c1 and c2 |
| c + 1.7 | Returns the sum of c and 1.7 |
| 1.7 + c | Returns the sum of 1.7 and c |
| c1 - c2 | Returns the difference between c1 and c2 |
| c - 1.7 | Returns the difference between c and 1.7 |
| 1.7 - c | Returns the difference between 1. 7 and c |
| c1 * c2 | Returns the product of c1 and c2 |
| c * 1.7 | Returns the product of c and 1.7 |
| 1.7 * c | Returns the product of 1.7 and c |
| c1 / c2 | Returns the quotient of c1 and c2 |
| c / 1.7 | Returns the quotient of c and 1.7 |
| 1.7 / c | Returns the quotient of 1.7 and c |
| - c | Returns the negated value of c |
| + c | Returns c |
| c1 += c2 | Equivalent to c1 = c1 + c2 |
| c1 -= c2 | Equivalent to c1 = c1 - c2 |
| c1 *= c2 | Equivalent to c1 = c1 * c2 |
| c1 /= c2 | Equivalent to c1 = c1 / c2 |
Class complex provides the common I/O operators << and >> (Table 12.6).
| Expression | Effect |
|---|---|
| strm << c | Writes the complex number c to the ostream strm |
| strm >> c | Reads the complex number c from the istream strm |
The output operator writes the complex number with respect to the actual stream state with the format:
(realpart, imagpart)
In particular, the output operator is defined as equivalent to the following implementation:
template <class T, class charT, class traits>
std::basic_ostream<charT, traits>&
operator<< (std::basic_ostream<charT, traits>& strm,
const std::complex<T>& c)
{
// temporary value string to do the output with one argument
std::basic_ostringstream<charT, traits> s;
s.flags (strm.flags()); // copy stream flags
s.imbue (strm.getloc()); // copy stream locale
s.precision(strm.precision()); // copy stream precision
// prepare the value string
s << '(' << c.real() << ',' << c.imag() << ')' << std::ends;
// write the value string
strm << s.str();
return strm;
}
The input operator provides the ability to read a complex number with one of the following formats:
(realpart, imagpart) (realpart) realpart
If none of the formats fits according to the next characters in the input stream, the ios::failbit is set, which might throw a corresponding exception (see Section 13.4.4,).
Unfortunately, you can't specify the separator of complex numbers between the real and the imaginary parts. So if you have a comma as a "decimal point" (as is the case in German), I/O looks really strange. For example, a complex number with 4.6 as the real part and 2.7 as the imaginary part would be written as
(4,6,2,7)
See page 532 for an example of how to use the I/O operations.
Table 12.7 lists the transcendental functions (trigonometric, exponential, and so on) for complex.
| Expression | Effect |
|---|---|
| pow(c, 3) | Complex power c3 |
| pow(c, 1.7) | Complex power c1.7 |
| pow(c1, c2) | Complex power c1c2 |
| pow(1.7, c) | Complex power 1.7C |
| exp(c) | Base e exponential of c (ec) |
| sqrt(c) | Square root of c ( |
| log(c) | Complex natural logarithm of c with base e (ln c) |
| log10(c) | Complex common logarithm of c with base 10 (lg c) |
| sin(c) | Sine of c (sin c) |
| cos(c) | Cosine of c (cos c) |
| tan(c) | Tangent of c (tan c) |
| sinh(c) | Hyperbolic sine of c (sinh c) |
| cosh(c) | Hyperbolic cosine of c (cosh c) |
| tanh(c) | Hyperbolic tangent of c (tanh c) |
This subsection describes all operations of class complex<> in detail. In the following definitions, T is the template parameter of class complex<>, which is the type of the real and the imaginary parts of the complex value.
complex:: value_type
The type of the real and the imaginary parts.
complex::complex ()
The default constructor.
Creates a complex value in which the real and the imaginary parts are initialized by an explicit call of their default constructor. Thus, for fundamental types, the initial value of the real and the imaginary parts is 0 (see page 14 for the default value of fundamental types).
complex::complex (const T& re)
Creates a complex value in which re is the value of the real part, and the imaginary part is initialized by an explicit call of its default constructor (0 for fundamental data types).
This constructor also defines an automatic type conversion from T to complex.
complex::complex (const T& re, const T& im)
Creates a complex value, with re as the real part and im as the imaginary part.
complex polar (const T& rho)
complex polar (const T& rho, const T& theta)
Both forms create and return the complex number that is initialized by polar coordinates.
rho is the magnitude.
theta is the phase angle in radians (default: 0).
complex conj (const complex& cmplx)
Creates and returns the complex number that is initialized by the conjugated complex value (the value with the negated imaginary part) of cmplx.
complex :: complex (const complex& cmplx)
The copy constructor.
Creates a new complex as a copy of cmplx.
Copies the real and imaginary parts.
In general, this function is provided as both a nontemplate and a template function (see page 11 for an introduction to member templates). Thus, in general, automatic type conversions of the element type are provided.
However, the specializations for float, double, and long double restrict copy constructors, so the less safe conversions from double and long double to float, as well as from long double to double, must be explicit and allow no other element type conversions:
namespace std {
template<> class complex<float> {
public:
explicit complex(const complex<double>&);
explicit complex(const complex<long double>&);
// no other kinds of copy constructors
...
};
template<> class complex<double> {
public:
complex(const complex<float>&);
explicit complex(const complex<long double>&);
// no other kinds of copy constructors
...
};
template<> class complex<long double> {
public:
complex(const complex<float>&);
complex(const complex<double>&);
// no other kinds of copy constructors
...
};
}
See page 534 for more information about the implications from this.
complex& complex::operator = (const complex& cmplx)
Assigns the value of complex cmplx.
Returns *this.
This function is provided as both a nontemplate and a template function (see page 11 for an introduction to member templates). Thus, automatic type conversions of the element type are provided. (This is also the case for the specializations that are provided by the C++ standard library.)
complex& complex::operator += (const complex& cmplx)
complex& complex::operator -= (const complex& cmplx)
complex& complex::operator *= (const complex& cmplx)
complex& complex::operator /= (const complex& cmplx)
These operations add, subtract, multiply, and divide the value of cmplx to, from, by, and into *this respectively and store the result in *this.
They return *this.
These operations are provided as both a nontemplate and a template function (see page 11 for an introduction to member templates). Thus, automatic type conversions of the element type are provided. (This is also the case for the specializations that are provided by the C++ standard library.)
Note that the assignment operators are the only functions that allow you to modify the value of an existing complex.
T complex :: real () const
T real (const complex& cmplx)
T complex::imag () const
T imag (const complex& cmplx)
These functions return the real or imaginary part respectively.
Note that the return value is not a reference. Thus, you can't use these functions to modify the real or the imaginary parts. To change only the real part or only the imaginary part you must assign a new complex number (see page 536).
T abs (const complex& cmplx)
Returns the absolute value (magnitude) of cmplx.
The absolute value is
![]()
T norm (const complex& cmplx)
Returns the squared absolute value (squared magnitude) of cmplx.
The squared absolute value is cmplx.real()2 + cmplx.imag()2.
T arg (const complex& cmplx)
Returns the angle of the polar representation
![]() of cmplx in radians.
of cmplx in radians.
It is equivalent to atan2(cmplx.imag(), cmplx.real()) as the phase angle.
ostream& operator << (ostream& strm, const complex& cmplx)
Writes the value of cmplx to the stream strm in the format (realpart, imagpart)
See page 539 for the exact behavior of this operation.
istream& operator >> (istream& strm, complex& cmplx)
Reads a new value from strm into cmplx.
Valid input formats are
(realpart, imagpart)
(realpart)
realpart
See page 539 for the exact behavior of this operation.
complex operator+ (const complex& cmplx)
The positive sign.
Returns cmplx.
complex operator- (const complex& cmplx)
The negative sign.
Returns the value of cmplx with the negated real and the negated imaginary parts.
complex binary-op (const complex& cmplx1, const complex& cmplx2)
complex binary-op (const complex& cmplx, const T& value)
complex binary-op (const T& value, const complex& cmplx)
All forms return a complex number with the result ofbinary-op.
binary-op may be any of the following:
operator + operator - operator * operator /
If a scalar value of the element type is passed, it is interpreted as the real part, with the imaginary part having the default value of its type (which is 0 for fundamental types).
bool comparison (const complex& cmplx1, const complex&, cmplx2)
bool comparison (const complex& cmplx, const T& value)
bool comparison (const T& value, const complex& cmplx)
Returns the result of the comparison of two complex numbers or the result of the comparison of a complex number with a scalar value.
comparison may be any of the following:
operator == operator !=
If a scalar value of the element type is passed, it is interpreted as the real part, with the imaginary part having the default value of its type (which is 0 for fundamental types).
Note that no operators <, <=, >, and >= are provided.
complex pow (const complex& base, int exp)
complex pow (const complex& base, const T& exp)
complex pow (const complex& base, const complex& exp)
complex pow (const T& base, const complex& exp)
All forms return the complex power of base raised to the expth power, defined as exp (exp*log(base)).
The branch cuts are along the negative real axis.
The value returned for pow (0,0) is implementation defined.
complex exp (const complex& cmplx)
Returns the complex base e exponential of cmplx.
complex sqrt (const complex& cmplx)
Returns the complex square root of cmplx in the range of the right halt plane.
If the argument is a negative real number, the value returned lies on the positive imaginary axis.
The branch cuts are along the negative real axis.
complex log (const complex& cmplx)
Returns the complex natural base e logarithm of cmplx.
When cmplx is a negative real number, imag(log(cmplx)) is pi.
The branch cuts are along the negative real axis.
complex log10 (const complex& cmplx)
Returns the complex base 10 logarithm of cmplx.
It is equivalent to log(cmplx)/log(10).
The branch cuts are along the negative real axis.
complex sin (const complex& cmplx)
complex cos (const complex& cmplx)
complex tan (const complex& cmplx)
complex sinh (const complex& cmplx)
complex cosh (const complex& cmplx)
complex tanh (const complex& cmplx)
These operations return the corresponding complex trigonometric operation on cmplx.
The C++ standard library provides the class valarray for the processing of arrays of numeric values. A valarray is a representation of the mathematical concept of a linear sequence of values. It has one dimension, but you can get the illusion of higher dimensionality by special techniques of computed indices and powerful subsetting capabilities. Therefore, a valarray can be used as a base both for vector and matrix operations as well as for the processing of mathematical systems of polynomial equations with good performance.
The valarray classes enable some tricky optimizations to get good performance for the processing of value arrays. However, it is not clear how important this component of the C++ standard library will be in the future because there are other interesting developments that perform even better. One of the most interesting examples is the Blitz system. If you are interested in numeric processing, you should look at it. For details, see http://monet.uwaterloo.ca/blitz/.
The valarray classes were not designed very well. In fact, nobody tried to determine whether the final specification worked. This happened because nobody felt "responsible" for these classes. The people who introduced valarrays to the C++ standard library left the committee a long time before the standard was finished. For example, to use valarrays, you often need some inconvenient and time-consuming type conversions (see page 554).
Valarrays are one-dimensional arrays with elements numbered sequentially from zero. They provide the ability to do some numeric processing for all or a subset of the values in one or more value arrays. For example, you can process the statement
z = a*x*x + b*x + c
with a, b, c, x, and z being arrays that contain hundreds of numeric values. In doing this, you have the advantage of a simple notation. Also, the processing is done with good performance because the classes provide some optimizations that avoid the creation of temporary objects while processing the whole statement. In addition, special interfaces and auxiliary classes provide the ability to process only a certain subset of value arrays or to do some multidimensional processing. In this way, the valarray concept also helps to implement vector and matrix operations and classes.
The standard guarantees that valarrays are alias free. That is, any value of a nonconstant valarray is accessed through a unique path. Thus, operations on these values can get optimized better because the compiler does not have to take into account that the data could be accessed through another path.
Valarrays are declared in the header file <valarray>:
#include <valarray>
In particular, in <valarray> the following classes are declared:
namespace std {
template<class T> class valarray; // numeric array of type T
class slice; // slice out of a valarray
template<class T> class slice_array;
class gslice; // a generalized slice
template<class T> class gslice_array;
template<class T> class mask_array; // a masked valarray
template<class T> class indirect_array; // an indirected valarray
}
The classes have the following meanings:
valarray is the core class that manages an array of numeric values.
slice and gslice arc provided to define a BLAS-like[4] slice as a subset of a valarray.
slice_array, gslice_array, mask_array, and indirect_array are internal auxiliary classes that are used to store temporary values or data. You can't use them in your programming interface directly. They are created indirectly by certain valarray operations.
All classes are templatized for the type of the elements. In principle, the type could be any data type. However, according to the nature of valarrays it should be a numeric data type.
When you create a valarray you usually pass the number of elements as a parameter:
std::valarray<int> va1(10); // valarray of ten ints with value 0 std::valarray<float> va2(5.7, 10); // valarray of ten floats with value 5.7 // (note the order)
If you pass one argument, it is used as the size. The elements are initialized by the default constructor of their type. Elements of fundamental data types are initialized by zero (see Section 2.2.2, for a description of why fundamental data types may be initialized by a default constructor). If you pass a second value, the first is used as the initial value for the elements, whereas the second specifies the number of elements. Note that the order of passing two arguments to the constructor differs from that of all other classes of the C++ standard library. All STL container classes use the first numeric argument as the number of elements and the second argument as the initial value.
You can also initialize a valarray with an ordinary array:
int array[] = { 3, 6, 18, 3, 22 };
// initialize valarray by elements of an ordinary array
std::valarray<int> va3(array, sizeof (array)/sizeof (array[0]));
// initialize by the second to the fourth element
std::valarray<int> va4(array+1, 3);
The valarray creates copies of the passed values. Thus, you can pass temporary data for initialization.
For valarrays, the subscript operator is defined to access the element of a valarray. As usual, the first element has the index 0:
va[0] = 3 * va[1] + va[2];
In addition, all ordinary numeric operators are defined (addition, subtraction, multiplication, modulo, negation, bit operators, comparison operators, and logical operators, as well as all assignment operators). These operators are called for each element in the valarrays that is processed by the operation. Thus, the result of a valarray operation is a valarray that has the same number of elements as the operands and that contains the result of the elementwise computation. For example, the statement
va1 = va2 * va3;
is equivalent to
va1[0] = va2[0] * va3[0]; va1[l] = va2[l] * va3[l]; va1[2] = va2[2] * va3[2]; ...
If the number of elements of the combined valarrays differs, the result is undefined.
Of course, the operations are available only if the element's type supports them. And the exact meaning of the operation depends on the meaning of the operation for the elements. Thus, all of these operations simply do the same for each element or pair of elements in the valarrays they process.
For binary operations, one of the operands may be a single value of the element's type. In this case, the single value is combined with each element of the valarray that is used as the other operand. For example, the statement
va1 = 4 * va2;
is equivalent to
va1[0] = 4 * va2[0]; va1[1] = 4 * va2[l]; va1[2] = 4 * va2[2]; ...
Note that the type of the single value has to match exactly the element type of the valarray. Thus, the previous example works only if the element type is int. The following statement would fail:
std::valarray<double> va(20);
...
va = 4 * va; // ERROR: type mismatch
The schema of binary operations also applies to comparison operators. Thus, operator == does not return a single Boolean value that shows whether both valarrays are equal. Instead, it returns a new valarray with the same number of elements of type bool, where each value is the result of the individual comparison. For example, in the following code
std::valarray<double> val(10); std::valarray<double> va2(10); std::valarray<bool> vab(10); ... vab = (va1 == va2);
the last statement is equivalent to
vab[0] = (va1[0] == va2[0]); vab[1] = (va1[1] == va2[1]); vab[2] = (va1[2] == va2[2]); ... vab[9] = (va1 [9] == va2[9]);
For this reason, you can't sort valarrays by using operator <, and you can't use them as elements in STL containers if the test for equality is performed with operator == (see Section 5.10.1, for the requirements of elements of STL containers).
The following program demonstrates a simple use of valarrays:
// num/val1.cpp #include <iostream> #include <valarray> using namespace std; // print valarray template <class T> void printValarray (const valarray<T>& va) { for (int i=0; i<va.size(); i++) { cout << va[i] << ' '; } cout << endl; } int main() { // define two valarrays with ten elements valarray<double> va1(10), va2(10); // assign values 0.0, 1.1, up to 9.9 to the first valarray for (int i=0; i<10; i++) { va1[i] = i * 1.1; } // assign -1 to all elements of the second valarray va2 = -1; // print both valarrays printValarray(va1); printValarray(va2); // print minimum, maximum, and sum of the first valarray cout << "min(): " << val.min() << endl; cout << "max(): " << val.max() << endl; cout << "sum(): " << val.sum() << endl; // assign values of the first to the second valarray va2 = va1; // remove all elements of the first valarray va1.resize (0); // print both valarrays again printValarray(va1); printValarray(va2); }
The program has the following output:
0 1.1 2.2 3.3 4.4 5.5 6.6 7.7 8.8 9.9 -1 -1 -1 -1 -1 -1 -1 -1 -1 -1 min():0 max(): 9.9 sum(): 49.5 0 1.1 2.2 3.3 4.4 5.5 6.6 7.7 8.8 9.9
The transcendental operations (trigonometric and exponential) are defined as equivalent to the numeric operators. The operations are performed with all elements in the valarrays, and for binary operations, one of the operands may be a single value, which is used as one operand, with all elements of the valarrays as the other operand.
All of these operations are defined as global functions instead of member functions. This is to provide automatic type conversion for subsets of valarrays for both operands (subsets of valarrays are covered in Section 12.2.2,).
Here is a second example of the use of valarrays. It demonstrates the use of transcendental operations:
// num/val2.cpp #include <iostream> #include <valarray> using namespace std; // print valarray template <class T> void printValarray (const valarray<T>& va) { for (int i=0; i<va.size(); i++) { cout << va[i] << ' '; } cout << endl; } int main() { // create and initialize valarray with nine elements valarray<double> va(9); for (int i=0; i<va.size(); i++) { va[i] = i * 1.1; } // print valarray printValarray(va); // double values in the valarray va *= 2.0; // print valarray again printValarray(va); // create second valarray initialized by the values of the first plus 10 valarray<double> vb(va+10.0); // print second valarray printValarray(vb); // create third valarray as a result of processing both existing valarrays valarray<double> vc; vc = sqrt(va) + vb/2.0 - 1.0; // print third valarray printValarray(vc); }
The program has the following output:
0 1.1 2.2 3.3 4.4 5.5 6.6 7.7 8.8 0 2.2 4.4 6.6 8.8 11 13.2 15.4 17.6 10 12.2 14.4 16.6 18.8 21 23.2 25.4 27.6 4 6.58324 8.29762 9.86905 11.3665 12.8166 14.2332 15.6243 16.9952
The subscript operator [] is overloaded for special auxiliary objects of valarrays. These auxiliary objects define subsets of valarrays in different ways. In doing this, they provide an elegant way to operate on certain subsets of valarrays (with both read and write access).
The subset of a valarray is defined by using a certain subset definition as the index. For example:
va[std::slice (2, 4, 3)] // four elements with distance 3 starting from index 2 va[va>7] // all elements with a value greater than 7
If a subset definition such as std::slice(2, 4, 3) or va>7 is used with a constant valarray, the expression returns a new valarray with the corresponding elements. However, if such a subset definition is used with a nonconstant valarray, the expression returns a temporary object of a special auxiliary valarray class. This temporary object does not contain the subset values, only the definition of the subset. Thus, the evaluation of expressions is deferred until the values are needed to compute a final result.
This mechanism is called lazy evaluation. It has the advantage that no temporary values for expressions are computed. This saves time and memory. In addition, the technique provides reference semantics. Thus, the subsets are logical sets of references to the original values. You can use these subsets as the destination (lvalue) of a statement. For example, you could assign one subset of a valarray the result of a multiplication of two other subsets of the same valarray (examples follow shortly).
However, because "temporaries" are avoided, some unexpected conditions might occur when elements in the destination subset are also used in a source subset. Therefore, any operation of valarrays is guaranteed to work only if the elements of the destination subset and the elements of all source subsets are distinct.
With smart definitions of subsets you can give valarrays the semantics of two or more dimensions. Thus, in a way, valarrays may be used as multidimensional arrays.
There are four ways to define subsets of valarrays:
Slices
General slices
Masked subsets
Indirect subsets
The following subsections discuss them and give examples.
Before I start with the individual subsets, I have to mention a general problem. The handling of valarray subsets is not well designed. You can create subsets easily, but you can't combine them easily with other subsets. Unfortunately, you almost always need an explicit type conversion to valarray. This is because the C++ standard library does not specify that valarray subsets provide the same operations as valarrays.
For example, to multiply two subsets and assign the result to a third subset, you can't write the following:
// ERROR: conversions missing
va[std::slice(0,4,3)]
= va[std::slice (1,4,3)] * va[std::slice (2,4,3)];
Instead, you have to code by using a new-style cast (see page 19)[5]:
va[std::slice (0,4,3)]
= static_cast<std::valarray<double> >(va[std::slice (l,4,3)]) *
static_cast<std::valarray<double> >(va[std::slice (2,4,3)]);
or by using an old-style cast:
va[std::slice(0,4,3)]
= std::valarray<double>(va[std::slice (1,4,3)]) *
std::valarray<double>(va[std::slice (2,4,3)]);
This is tedious and error prone. Even worse, without good optimization it may cost performance because each cast creates a temporary object, which could be avoided without the cast.
To make the handling a bit more convenient, you can use the following template function:
/* template to convert valarray subset into valarray
*/
template <class T>
inline
std::valarray<typename T::value_type> VA (const T& valarray_subset)
{
return std::valarray<typename T::value_type>(valarray_subset);
}
By using this template, you could write
va[std::slice (0,4,3)] = VA(va[std::slice (l,4,3)]) *
VA(va[std::slice (2,4,3)]); // OK
However, the performance penalty remains.
If you use a certain element type you could also use a simple type definition:
typedef valarray<double> VAD;
By using this type definition you could also write
va[std::slice (0,4,3)] = VAD(va[std::slice(l,4,3)]) *
VAD (va[std:: slice (2,4,3)]); // OK
provided the elements of va have type double.
A slice defines a set of indices that has three properties:
The starting index
The number of elements (size)
The distance between elements (stride)
You can pass these three properties exactly in the same order as parameters to the constructor of class slice. For example, the following expression specifies four elements, starting with index 2 with distance 3:
std::slice (2,4,3)
In other words, the expression specifies the following set of indices:
2 5 8 11
The stride may be negative. For example, the expression
std::slice (9,5,-2)
specifies the following indices:
9 7 5 3 1
To define the subset of a valarray, you simply use a slice as an argument of the subscript operator. For example, the following expression specifies the subset of the valarray va that contains the elements with the indices 2, 5, 8, and 11:
va[std::slice (2,4,3)]
It's up to the caller to ensure that all these indices are valid.
If the subset qualified by a slice is a subset of a constant valarray, the subset is a new valarray. If the valarray is nonconstant, the subset has reference semantics to the original valarray. The auxiliary class slice_array is provided for this:
namespace std {
class slice;
template <class T>
class slice_array;
template <class T>
class valarray {
public:
// slice of a constant valarray returns a new valarray
valarray<T> operator[] (slice) const;
// slice of a variable valarray returns a slice_array
slice_array<T> operator[] (slice);
...
};
}
For slice_arrays, the following operations are defined:
Assign a single value to all elements.
Assign another valarray (or valarray subset).
Call any computed assignment operation, such as operators += and *=.
For any other operation you have to convert the subset to a valarray (see page 554). Note that the class slice_array<> is intended purely as an internal helper class for slices, and it should be transparent to the user. Thus, all constructors and the assignment operator of class slice_array<> are private.
For example, the statement
va[std::slice (2,4,3)] = 2;
assigns 2 to the third, sixth, ninth, and twelfth elements of the valarray va. It is equivalent to the following statements:
va[2] = 2; va[5] = 2; va[8] = 2; va[11] = 2;
As another example, the following statement squares the values of the elements with index 2, 5, 8, and 11:
va[std::slice (2,4,3)]
*= std::valarray<double>(va[std::slice(2,4,3)]);
As mentioned on page 554, you can't write
va[std::slice (2,4,3)] *= va[std::slice (2,4,3)]; // ERROR
But using the VA() template function mentioned on page 555, you can write
va[std::slice(2,4,3)] *= VA(va[std::slice (2,4,3)]);. // OK
By passing different slices of the same valarray you can combine different subsets and store the result in another subset of the valarray. For example, the statement
va[std::slice (0,4,3)] = VA(va[std::slice (l,4,3)]) *
VA(va[std::slice (2,4,3)]);
is equivalent to the following:
va[0] = va[1] * va[2]; va[3] = va[4] * va[5]; va[6] = va[7] * va[8]; va[9] = va[10] * va[11];
If you consider your valarray as a two-dimensional matrix, this example is nothing else but vector multiplication (Figure 12.1). However, note that the order of the individual assignments is not defined. Therefore, the behavior is undefined if the destination subset contains elements that are used in the source subsets.
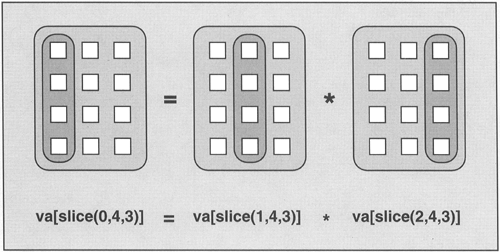
In the same way, more complicated statements are possible. For example:
va[std::slice (0,100,3)]
= std::pow(VA(va[std::slice (l,100,3)]) * 5.0,
VA(va[std::slice (2,100,3)]));
Note again that a single value, such as 5.0 in this example, has to match the element type of the valarray exactly.
The following program demonstrates a complete example of using valarray slices:
// num/slice1.cpp #include <iostream> #include <valarray> using namespace std; // print valarray line-by-line template<class T> void printValarray (const valarray<T>& va, int num) { for (int i=0; i<va.size()/num; ++i) { for (int j=0; j<num; ++j) { cout << va[i*num+j] << ' '; } cout << endl; } cout << endl; } int main() { /* valarray with 12 elements * - four rows * - three columns */ valarray<double> va(12); // fill valarray with values for (int i=0; i<12; i++) { va[i] = i; } printValarray (va, 3); // first column = second column raised to the third column va [slice (0,4,3)] = pow (valarray<double>(va[slice (l,4,3)]), valarray<double>(va[slice (2,4,3)])); printValarray (va, 3); // create valarray with three times the third element of va valarray<double> vb(va[slice (2,4,0)]); // multiply the third column by the elements of vb va[slice (2,4,3)] *= vb; printValarray (va, 3); // print the square root of the elements in the second row printValarray (sqrt(valarray<double>(va[slice (3,3,1)])), 3); // double the elements in the third row va[slice (2,4,3)] = valarray<double>(va[slice (2,4,3)]) * 2.0; printValarray (va, 3); }
The program has the following output:
0 1 2 3 4 5 6 7 8 9 10 11 1 1 2 1024 4 5 5.7648e+006 7 8 1e+011 10 11 1 1 4 1024 4 10 5.7648e+006 7 16 1e+011 10 22 32 2 3.16228 1 1 8 1024 4 20 5.7648e+006 7 32 1e+011 10 44
General slices, or gslices, are the general form of slices. Similar to slices, which provide the ability to handle a subset that is one dimension out of two dimensions, gslices allow the handling of subsets of multidimensional arrays. In principle, gslices have the same properties as slices:
Starting index
Number of elements (size)
Distance between elements (stride)
Unlike slices, however, the number and distance of elements in a gslice are arrays of values. The number of elements in such an array is equivalent to the number of dimensions used. For example, if a gslice has the state
start: 2 size: [ 4 ] stride: [ 3 ]
then the gslice is equivalent to a slice because the array handles one dimension. Thus, it defines four elements with distance 3, starting with index 2:
2 5 8 11
However, if a gslice has the state
start: 2 size: [ 2 4] stride: [ 10 3]
then the gslice handles two dimensions. The smallest index handles the highest dimension. Thus, this gslice specifies starting from index 2, twice with distance 10, four elements with distance 3:
2 5 8 11 12 15 18 21
Here is an example of a slice with three dimensions:
start: 2 size: [ 3 2 4 ] stride: [ 30 10 3 ]
It specifies starting from index 2, three times with distance 30, twice with distance 10, four elements with distance 3:
2 5 8 11 12 15 18 21 32 35 38 41 42 45 48 51 62 65 68 71 72 75 78 81
The ability to use arrays to define size and stride is the only difference between gslices and slices. Apart from this, gslices behave the same as slices:
To define a concrete subset of a valarray, you simply pass a gslice as the argument to the subscript operator of the valarray.
If the valarray is constant, the resulting expression is a new valarray.
If the valarray is nonconstant, the resulting expression is a gslice_array that represents the elements of the valarray with reference semantics:
namespace std {
class gslice;
template <class T>
class gslice_array;
template <class T>
class valarray {
public:
// gslice of a constant valarray returns a new valarray
valarray<T> operator[] (const gslice&) const;
// gslice of a variable valarray returns a gslice_array
gslice_array<T> operator[] (const gslice&);
...
};
}
For gslice_array, the assignment and computed assignment operators are provided to modify the elements of the subset.
By using type conversions you can combine a gslice array with other valarrays and subsets of valarrays (see page 554).
The following program demonstrates the use of valarray gslices:
// num/gslice1.cpp #include <iostream> #include <valarray> using namespace std; // print three-dimensional valarray line-by-line template<class T> void printValarray3D (const valarray<T>& va, int dim1, int dim2) { for (int i=0; i<va.size()/(dim1*dim2); ++i) { for (int j=0; j<dim2; ++j) { for (int k=0; k<dim1; ++k) { cout << va[i*dim1*dim2+j*dim1+k] << ' '; } cout << '\n'; } cout << '\n'; } cout << endl; } int main() { /* valarray with 24 elements * - two groups * -four rows * - three columns */ valarray<double> va(24); // fill valarray with values for (int i=0; i<24; i++) { va[i] = i; } // print valarray printValarray3D (va, 3, 4); // we need two two-dimensional subsets of three times 3 values // in two 12-element arrays size_t lengthvalues[] = { 2, 3 }; size_t stridevalues[] = { 12, 3 }; valarray<size_t> length(lengthvalues, 2); valarray<size_t> stride(stridevalues, 2); // assign the second column of the first three rows // to the first column of the first three rows va[gslice (0, length, stride)] = valarray<double>(va[gslice (1, length, stride)]); // add and assign the third of the first three rows // to the first of the first three rows va[gslice (0, length, stride)] += valarray<double>(va[gslice (2, length, stride)]); // print valarray printValarray3D (va, 3, 4); }
The program has the following output:
0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 3 1 2 9 4 5 15 7 8 9 10 11 27 13 14 33 16 17 39 19 20 21 22 23
Mask arrays provide another way to define a subset of a valarray. You can mask the elements with a Boolean expression. For example, in the expression
va[va > 7]
the subexpression
va > 7
returns a valarray with the size of va, where for each element a Boolean value states whether the element is greater than 7. The Boolean valarray is used by the subscript operator to specify all elements for which the Boolean expression yields true. Thus,
va[va > 7]
specifies the subset of elements in the valarray va that is greater than 7.
Apart from this, mask arrays behave the same as all valarray subsets:
To define a concrete subset of a valarray, you simply pass a valarray of Boolean values as the argument to the subscript operator of the valarray.
If the valarray is constant, the resulting expression is a new valarray.
If the valarray is nonconstant, the resulting expression is a mask_array that represents the elements of the valarray with reference semantics:
namespace std {
template <class T>
class mask_array;
template <class T>
class valarray {
public:
// masking a constant valarray returns a new valarray
valarray<T> operator[] (const valarray<bool>&) const;
// masking a variable valarray returns a mask_array
mask_array<T> operator[] (const valarray<bool>&);
...
};
}
For mask_array, the assignment and computed assignment operators are provided to modify the elements of the subset.
By using type conversions you can combine a mask array with other valarrays and subsets of valarrays (see page 554).
The following program demonstrates the use of masked subsets of valarrays:
// num/masked1.cpp #include <iostream> #include <valarray> using namespace std; // print valarray line-by-line template<class T> void printValarray (const valarray<T>& va, int num) { for (int i=0; i<va.size()/num; ++i) { for (int j=0; j<num; ++j) { cout << va[i*num+j] << ' '; } cout << endl; } cout << endl; } int main() { /* valarray with 12 elements * - four rows * - three columns */ valarray<double> va(12); // fill valarray with values for (int i=0; i<12; i++) { va[i] = i; } printValarray (va, 3); // assign 77 to all values that are less than 5 va[va<5.0] = 77.0; // add 100 to all values that are greater than 5 and less than 9 va[va>5.0 && va9.0] = valarray<double>(va[va>5.0 && va<9.0]) + 100.0; printValarray (va, 3); }
The program has the following output:
0 1 2 3 4 5 6 7 8 9 10 11 77 77 77 77 77 5 106 107 108 9 10 11
Note that the type of a numeric value that is compared with the valarray has to match the type of the valarray exactly. So, using an int value to compare it with a valarray of doubles would not compile:
valarray<double> va(12);
...
va[va<5] = 77; // ERROR
The fourth and last way to define a subset of a valarray is provided by indirect arrays. Here you simply define the subset of a valarray by passing an array of indices. Note that the indices that specify the subset don't have to be sorted and may occur twice.
Apart from this, indirect arrays behave the same as all valarray subsets:
To define a concrete subset of a valarray you simply pass a valarray of elements of type size_t as the argument to the subscript operator of the valarray.
If the valarray is constant, the resulting expression is a new valarray.
If the valarray is nonconstant, the resulting expression is an indirect_array that represents the elements of the valarray with reference semantics:
namespace std {
template <class T>
class indirect_array;
template <class T>
class valarray {
public:
// indexing a constant valarray returns a new valarray
valarray<T> operator[] (const valarray<bool>&) const;
// indexing a variable valarray returns a indirect_array
indirect_array<T> operator[] (const valarray<bool>&);
...
};
}
For indirect_array, the assignment and computed assignment operators are provided to modify the elements of the subset.
By using type conversions you can combine an indirect array with other valarrays and subsets of valarrays (see page 554).
The following program demonstrates how to use indirect arrays:
// num/indi1.cpp #include <iostream> #include <valarray> using namespace std; // print valarray as two-dimensional array template<class T> void printValarray (const valarray<T>& va, int num) { for (int i=0; i<va.size()/num; i++) { for (int j=0; j<num; j++) { cout << va[i*num+j] << ' '; } cout << endl; } cout << endl; } int main() { // create valarray for 12 elements valarray<double> va(12); // initialize valarray by values 1.01, 2.02, ... 12.12 for (int i=0; i<12; i++) { va[i] = (i+1) * 1.01; } printValarray(va, 4); /* create array of indexes * - note: element type has to be size_t */ valarray<size_t> idx(4); idx[0] = 8; idx[1] = 0; idx[2] = 3; idx[3] = 7; // use array of indexes to print the ninth, first, fourth, and eighth elements printValarray(valarray<double>(va[idx]), 4); // change the first and fourth elements and print them again indirectly va[0] = 11.11; va[3] = 44.44; printValarray(valarray<double>(va[idx]), 4); // now select the second, third, sixth, and ninth elements // and assign 99 to them idx[0] = 1; idx[l] = 2; idx[2] = 5; idx[3] = 8; va[idx] = 99; // print the whole valarray again printValarray (va, 4); }
The valarray idx is used to define the subset of the elements in valarray va. The program has the following output:
1.01 2.02 3.03 4.04 5.05 6.06 7.07 8.08 9.09 10.1 11.11 12.12 9.09 1.01 4.04 8.08 9.09 11.11 44.44 8.08 11.11 99 99 44.44 5.05 99 7.07 8.08 99 10.1 11.11 12.12
The class valarray<> is the core part of the valarray component. It is defined as a template class parameterized on the type of the elements:
namespace std {
template <class T>
class valarray;
}
The size is not part of the type. Thus, in principle you can process valarrays with different sizes and you can change the size. However, changing the size of a valarray is provided only to make a two-step initialization (creating and setting the size), which you can't avoid to manage arrays of valarrays. Beware that the result of combining valarrays of different size is undefined.
valarray::valarray ()
The default constructor.
Creates an empty valarray.
This constructor is provided only to enable the creation of arrays of valarrays. The next step is to give them the correct size using the resize() member function.
explicit valarray::valarray (size_t num)
Creates a valarray that contains num elements.
The elements are initialized by their default constructor (which is 0 for fundamental data types).
valarray::valarray (const T& value, size_t num)
Creates a valarray that contains num elements.
The elements are initialized by value.
Note that the order of parameters is unusual. All other classes of the C++ standard library provide an interface in which num is the first parameter and value is the second parameter.
valarray::valarray (const T* array, size_t num)
Creates a valarray that contains num elements.
The elements are initialized by the values of the elements in array.
The caller must ensure that array contains num elements; otherwise, the behavior is undefined.
valarray::valarray (const valarray& va)
The copy constructor.
Creates a valarray as a copy of va.
valarray::~valarray ()
The destructor.
Destroys all elements and frees the memory.
In addition, you can create valarrays initialized by objects of the internal auxiliary classes slice_array, gslice_array, mask_array, and indirect_array. See pages 575, 577, 578, and 579, respectively, for details about these classes.
valarray& valarray::operator = (const valarray& va)
Assigns the elements of the valarray va.
If va has a different size, the behavior is undefined.
The value of an element on the left side of any valarray assignment operator should not depend on the value of another element on that left side. In other words, if an assignment overwrites values that are used on the right side of the assignment, the result is undefined. This means you should not use an element on the left side anywhere in the expression on the right side. The reason for this is that the order of the evaluation of valarray statements is not defined. See page 557 and page 554 for details.
valarray& valarray::operator = (const T& value)
Assigns value to each element of the valarray.[6]
The size of the valarray is not changed. Pointers and references to the elements remain valid.
In addition, you can assign values of the internal auxiliary classes slice_array, gslice_array, mask_array, and indirect_array. See pages 575, 577, 578, and 579, respectively, for details about these classes.
Class valarray provides the following member functions.
size_t valarray::size () const
Returns the actual number of elements.[7]
void valarray::resize (size_t num)
void valarray::resize (size_t num, T value)
Both forms change the size of the valarray to num.
If the size grows, the new elements are initialized by their default constructor or with value respectively.
Both forms invalidate all pointers and references to elements of the valarray.
These functions are provided only to enable the creation of arrays of valarrays. After creating them with the default constructor you should give them the correct size by calling this function.
T valarray::min () const
T valarray::max () const
The first form returns the minimum value of all elements.
The second form returns the maximum value of all elements.
The elements are compared with operator < or >. Thus, these operators must be provided for the element type.
If the valarray contains no elements, the return value is undefined.
T valarray::sum () const
Returns the sum of all elements.
The elements are processed by operator +=. Thus, this operator has to be provided for the element type.
If the valarray contains no elements, the return value is undefined.
valarray valarray::shift (int num) const
Returns a new valarray in which all elements are shifted by num positions.
The returned valarray has the same number of elements.
Elements of positions that were shifted are initialized by their default constructor.
The direction of the shifting depends on the sign of num:
If num is positive, it shifts to the left/front. Thus, elements get a smaller index.
If num is negative, it shifts to the right/back. Thus, elements get a higher index.
valarray valarray::cshift (int num) const
Returns a new valarray in which all elements are shifted cyclically by num positions.
The returned valarray has the same number of elements.
The direction of the shifting depends on the sign of num:
If num is positive, it shifts to the left/front. Thus, elements get a smaller index or are inserted at the back.
If num is negative, it shifts to the right/back. Thus, elements get a higher index or are inserted at the front.
valarray valarray::apply (T op (T)) const
valarray valarray::apply (T op (const T&)) const
Both forms return a new valarray with all elements processed by op().
The returned valarray has the same number of elements.
For each element of *this, it calls op(elem) and initializes the corresponding element in the new returned valarray by its result.
T & valarray::operator [ ] (size_t idx)
T valarray::operator [ ] (size_t idx) const
Both forms return the valarray element that has index idx (the first element has index 0).
The nonconstant version returns a reference. So, you can modify the element that is specified and returned by this operator. The reference is guaranteed to be valid as long as the valarray exists, and no function is called that modifies the size of the valarray.
Unary valarray operators have the following format:
valarray valarray :: unary-op () const
A unary operator returns a new valarray that contains all values of *this modified by unary-op.
unary-op may he any of the following:
operator + operator - operator ~ operator !
The return type for operator ! is valarray<bool>.
The binary operators for valarrays (except comparison and assignment operators) have the following format:
valarray binary-op (const valarray& va1, const valarray& va2)
valarray binary-op (const valarray& va, const T& value)
valarray binary-op (const T& value, const valarray& va)
These operators return a new valarray with the same number of elements as va, va1, or va2. The new valarray contains the result of computing binary-op for each value pair.
If only one operand is passed as a single value, it is combined with each element of va.
binary-op may be any of the following:
operator + operator - operator * operator / operator % operator ~ operator & operator | operator << operator >>
If va1 and va2 have different numbers of elements, the result is undefined.
The logical and comparison operators follow the same schema. However, their return values are a valarray of Boolean values:
valarray<bool> logical-op (const valarray& va1, const valarray& va2)
valarray<bool> logical-op (const valarray& va, const T& value)
valarray<bool> logical-op (const T& value, const valarray& va)
These operators return a new valarray with the same number of elements as va, va1, or va2. The new valarray contains the result of computing logical-op for each value pair.
If only one operand is passed as a single value, it is combined with each element of va.
logical-op may be any of the following:
operator ==
operator !=
operator <
operator <=
operator >
operator >=
operator &&
operator ||
If va1 and va2 have different numbers of elements, the result is undefined.
Similarly, computed assignment operators are defined for valarrays:
valarray& valarray::assign-op (const valarray& va)
valarray& valarray::assign-op (const T& value)
Both forms call for each element in *this assign-op with the corresponding element of va or value, respectively, as the second operand.
They return a reference to the modified valarray.
assign-op may be any of the following:
operator +=
operator -=
operator *=
operator /=
operator %=
operator ^=
operator &=
operator |=
operator <<=
operator >>=
If *this and va2 have different numbers of elements, the result is undefined.
References and pointers to modified elements stay valid as long as the valarray exists, and no function is called that modifies the size of the valarray.
valarray abs (const valarray& va)
valarray pow (const valarray& va1, const valarray& va2)
valarray pow (const valarray& va, const T& value)
valarray pow (const T& value, const valarray& va)
valarray exp (const valarray& va)
valarray sqrt (const valarray& va)
valarray log (const valarray& va)
valarray log10 (const valarray& va)
valarray sin (const valarray& va)
valarray cos (const valarray& va)
valarray tan (const valarray& va)
valarray sinh (const valarray& va)
valarray cosh (const valarray& va)
valarray tanh (const valarray& va)
valarray asin (const valarray& va)
valarray acos (const valarray& va)
valarray atan (const valarray& va)
valarray atan2 (const valarray& va1, const valarray& va2)
valarray atan2 (const valarray& va, const T& value)
valarray atan2 (const T& value, const valarray& va)
All of these functions return a new valarray with the same number of elements as va, va1, or va2. The new valarray contains the result of the corresponding operation called for each element or pair of elements.
If va1 and va2 have different numbers of elements, the result is undefined.
This subsection describes the subset classes for valarray in detail. However, these classes are very simple and do not provide many operations, thus I provide only their declarations along with a few remarks.
Objects of class slice_array are created by using a slice as the index of a nonconstant valarray:
namespace std {
template<class T>
class valarray {
public:
...
slice_array<T> operator[] (slice);
...
};
}
The exact definition of the public interface of class slice is as follows:
namespace std {
class slice {
public:
slice (); // empty subset
slice (size_t start, size_t size, size_t stride);
size_t start() const;
size_t size() const;
size_t stride() const;
};
}
The default constructor creates an empty subset. With the start(), size(), and stride() member functions, you can query the properties of a slice.
The class slice_array provides the following operations:
namespace std {
template <class T>
class slice_array {
public:
typedef T value_type;
void operator= (const T&);
void operator= (const valarray<T>&) const;
void operator*= (const valarray<T>&) const;
void operator/= (const valarray<T>&) const;
void operator%= (const valarray<T>&) const;
void operator+= (const valarray<T>&) const;
void operator-= (const valarray<T>&) const;
void operator~= (const valarray<T>&) const;
void operator&= (const valarray<T>&) const;
void operator|= (const valarray<T>&) const;
void operator<<=(const valarray<T>&) const;
void operator>>=(const valarray<T>&) const;
~slice_array();
private:
slice_array();
slice_array(const slice_array&);
slice_array& operator=(const slice_array&);
...
};
}
Note that class slice_array<> is intended purely as an internal helper class for slices and should be transparent to the user. Thus, all constructors and the assignment operator of class slice_array<> are private.
Objects of class gslice_array are created by using a gslice as the index of a nonconstant valarray:
namespace std {
template<class T>
class valarray {
public:
...
gslice_array<T> operator[] (const gslice&);
...
};
}
The exact definition of the public interface of gslice is as follows:
namespace std {
class gslice {
public:
gslice (); // empty subset
gslice (size_t start,
const valarray<size_t>& size,
const valarray<size_t>& stride);
size_t start() const;
valarray<size_t> size() const;
valarray<size_t> stride() const;
};
}
The default constructor creates an empty subset. With the start(), size(), and stride() member functions you can query the properties of a gslice.
The class gslice_array provides the following operations:
namespace std {
template <class T>
class gslice_array {
public:
typedef T value_type;
void operator= (const T&);
void operator= (const valarray<T>&) const;
void operator*= (const valarray<T>&) const;
void operator/= (const valarray<T>&) const;
void operator%= (const valarray<T>&) const;
void operator+= (const valarray<T>&) const;
void operator-= (const valarray<T>&) const;
void operator~= (const valarray<T>&) const;
void operator&= (const valarray<T>&) const;
void operator|= (const valarray<T>&) const;
void operator<<=(const valarray<T>&) const;
void operator>>=(const valarray<T>&) const;
~gslice_array();
private:
gslice_array();
gslice_array(const gslice_array<T>&);
gslice_array& operator=(const gslice_array<T>&);
...
};
}
As with slice_array<>, note that class gslice_array<> is intended purely as an internal helper class for gslices and should be transparent to the user. Thus, all constructors and the assignment operator of class gslice_array<> are private.
Objects of class mask_array are created by using a valarray<bool> as the index of a nonconstant valarray:
namespace std {
template<class T>
class valarray {
public:
...
mask_array<T> operator[](const valarray<bool>&);
...
};
}
The class mask_array provides the following operations:
namespace std {
template <class T>
class mask_array {
public:
typedef T value_type;
void operator= (const T&);
void operator= (const valarray<T>&) const;
void operator*= (const valarray<T>&) const;
void operator/= (const valarray<T>&) const;
void operator%= (const valarray<T>&) const;
void operator+= (const valarray<T>&) const;
void operator-= (const valarray<T>&) const;
void operator^= (const valarray<T>&) const;
void operator&= (const valarray<T>&) const;
void operator|= (const valarray<T>&) const;
void operator<<=(const valarray<T>&) const;
void operator>>=(const valarray<T>&) const;
~mask_array();
private:
mask_array();
mask_array(const mask_array<T>&);
mask_array& operator=(const mask_array<T>&);
...
};
}
Again, note that class mask_array<> is intended purely as an internal helper class and should be transparent to the user. Thus, all constructors and the assignment operator of class mask_array<> are private.
Objects of class indirect_array are created by using a valarray<size_t> as the index of a nonconstant valarray:
namespace std {
template<class T>
class valarray {
public:
...
indirect_array<T> operator[](const valarray<size_t>&);
...
};
}
The class indirect_array provides the following operations:
namespace std {
template <class T>
class indirect_array {
public:
typedef T value_type;
void operator= (const T&);
void operator= (const valarray<T>&) const;
void operator*= (const valarray<T>&) const;
void operator/= (const valarray<T>&) const;
void operator%= (const valarray<T>&) const;
void operator+= (const valarray<T>&) const;
void operator-= (const valarray<T>&) const;
void operator~= (const valarray<T>&) const;
void operator&= (const valarray<T>&) const;
void operator|= (const valarray<T>&) const;
void operator<<=(const valarray<T>&) const;
void operator>>=(const valarray<T>&) const;
~indirect_array();
private:
indirect_array();
indirect_array(const indirect_array<T>&);
indirect_array& operator=(const indirect_array<T>&);
...
};
}
As usual, class indirect, array <> is intended purely as an internal helper class and should he transparent to the user. Thus, all constructors and the assignment operator of indirect_array<> are private.
The header files <cmath> and <cstdlib> provide the global numeric functions that are inherited from C. Tables 12.8 and 12.9 list these functions.[8]
| Function | Effect |
|---|---|
| pow() | Power function |
| exp() | Exponential function |
| sqrt() | Square root |
| log() | Natural logarithm |
| log10() | Base 10 logarithm |
| sin() | Sine |
| cos() | Cosine |
| tan() | Tangent |
| sinh() | Hyperbolic sine |
| cosh() | Hyperbolic cosine |
| tanh() | Hyperbolic tangent |
| asin() | Arc sine |
| acos() | Arc cosine |
| atan() | Arc tangent |
| atan2() | Arc tangent of a quotient |
| ceil() | Floating-point value rounded up to the next integral value |
| floor() | Floating-point value rounded down to the next integral value |
| fabs() | Absolute value of a floating-point value |
| fmod() | Remainder after division for floating-point value (modulo) |
| frexp() | Converts floating-point value to fractional and integral components |
| 1dexp() | Multiplies floating-point value by integral power of two |
| modf() | Extracts signed integral and fractional values from floating-point value |
In contrast to C, C++ overloads some operations for different types, which makes some numeric functions of C obsolete. For example, C provides abs(), labs(), and fabs() to process the absolute value of int, long, and double, respectively. In C++, abs() is overloaded for different data types so that you can use it for all data types.
| Function | Effect |
|---|---|
| abs() | Absolute value of an int value |
| labs() | Absolute value of a long |
| div() | Quotient and remainder of int division |
| ldiv() | Quotient and remainder of long division |
| srand() | Random number generator (seed new sequence) |
| rand() | Random number generator (next number of sequence) |
In particular, all numeric functions for floating-point values are overloaded for types float, double, and long double. However, this has an important side effect: When you pass an integral value, the expression is ambiguous:[9]:
std::sqrt(7) // AMBIGUOUS: sqrt (float), sqrt (double), or // sqrt (long double)?
Instead, you have to write
std::sqrt(7.0) // OK
or, if you use a variable, you must write
int x;
...
std::sqrt(float(x)) // OK
Library vendors handle this problem completely different: some don't provide the overloading, some provide standard conforming behavior (overload for all floating-point types), some overload for all numeric types, and some allow you to switch between different policies by using the preprocessor. Thus, in practice, the ambiguity might or might not occur. To write portable code, you should always write the code in a way that the arguments match exactly.
[1] The fact that constructors for the complex specializations allow only safe implicit conversions, whereas the assignment operations allow any implicit conversion, is probably a mistake in the standard.
[2] There is a minor difference between
X x; Y y(x); // explicit conversionand
X x; Y y = x; // implicit conversionThe former creates a new object of type Y by using an explicit conversion from type X, whereas the latter creates a new object of type Y by using an implicit conversion.
[3] Thanks to David Vandevoorde for pointing this out.
[4] The Basic Linear Algebra Subprograms (BLAS) library provides computational kernels for several of the fundamental linear algebra operations, such as matrix multiply, the solution of triangular systems, and simple vector operations.
[5] Note that you have to put a space between the two ">" characters. ">>" would be parsed as shift operator, which would result in a syntax error.
[6] In earlier versions single values were assigned by the member function fill().
[7] The member function size() was called length() in earlier versions.
[8] For historical reasons, some numeric functions are defined in <cstdlib> rather than in <cmath>.
[9] Thanks to David Vandevoorde for pointing this out.
| CONTENTS |
| Browser Based Help. Published by chm2web software. |