| CONTENTS |
The heart of the C++ standard library, the part that influenced its overall architecture, is the standard template library (STL). The STL is a generic library that provides solutions to managing collections of data with modern and efficient algorithms. It allows programmers to benefit from innovations in the area of data structures and algorithms without needing to learn how they work.
From the programmer's point of view, the STL provides a bunch of collection classes that meet different needs, together with several algorithms that operate on them. All components of the STL are templates, so they can be used for arbitrary element types. But the STL does even more: It provides a framework for supplying other collection classes or algorithms for which existing collection classes and algorithms work. All in all, the STL gives C++ a new level of abstraction. Forget programming dynamic arrays, linked lists, and binary trees; forget programming different search algorithms. To use the appropriate kind of collection, you simply define the appropriate container and call the member functions and algorithms to process the data.
The STL's flexibility, however, has a price, chief of which is that it is not self-explanatory. Therefore, the subject of the STL fills several chapters in this book. This chapter introduces the general concept of the STL and explains the programming techniques needed to use it. The first examples show how to use the STL and what to consider while doing so. Chapters 6 through 9 discuss the components of the STL (containers, iterators, function objects, and algorithms) in detail and present several more examples.
The STL is based on the cooperation of different well-structured components, key of which are containers, iterators, and algorithms:
Containers are used to manage collections of objects of a certain kind. Every kind of container has its own advantages and disadvantages, so having different container types reflects different requirements for collections in programs. The containers may be implemented as arrays or as linked lists, or they may have a special key for every element.
Iterators are used to step through the elements of collections of objects. These collections may be containers or subsets of containers. The major advantage of iterators is that they offer a small but common interface for any arbitrary container type. For example, one operation of this interface lets the iterator step to the next element in the collection. This is done independently of the internal structure of the collection. Regardless of whether the collection is an array or a tree, it works. This is because every container class provides its own iterator type that simply "does the right thing" because it knows the internal structure of its container.
The interface for iterators is almost the same as for ordinary pointers. To increment an iterator you call operator ++. To access the value of an iterator you use operator *. So, you might consider an iterator a kind of a smart pointer that translates the call "go to the next element" into whatever is appropriate.
Algorithms are used to process the elements of collections. For example, they can search, sort, modify, or simply use the elements for different purposes. Algorithms use iterators. Thus, an algorithm has to be written only once to work with arbitrary containers because the iterator interface for iterators is common for all container types.
To give algorithms more flexibility you can supply certain auxiliary functions called by the algorithms. Thus, you can use a general algorithm to suit your needs even if that need is very special or complex. For example, you can provide your own search criterion or a special operation to combine elements.
The concept of the STL is based on a separation of data and operations. The data is managed by container classes, and the operations are defined by configurable algorithms. Iterators are the glue between these two components. They let any algorithm interact with any container (Figure 5.1).
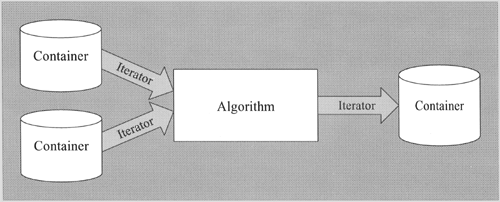
In a way, the STL concept contradicts the original idea of object-oriented programming: The STL separates data and algorithms rather than combining them. However, the reason for doing so is very important. In principle, you can combine every kind of container with every kind of algorithm, so the result is a very flexible but still rather small framework.
One fundamental aspect of the STL is that all components work with arbitrary types. As the name "standard template library" indicates, all components are templates for any type (provided the type is able to perform the required operations). Thus the STL is a good example of the concept of generic programming. Containers and algorithms are generic for arbitrary types and classes respectively.
The STL provides even more generic components. By using certain adapters and function objects (or functors) you can supplement, constrain, or configure the algorithms and the interfaces for special needs. However, I'm jumping the gun. First, I want to explain the concept step-by-step by using examples. This is probably the best way to understand and become familiar with the STL.
Container classes, or containers for short, manage a collection of elements. To meet different needs, the STL provides different kinds of containers, as shown in Figure 5.2.
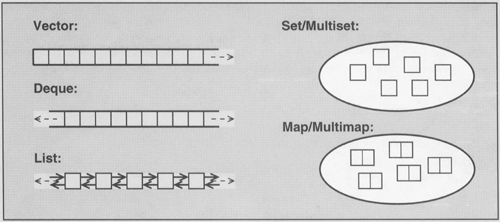
There are two general kinds of containers:
Sequence containers are ordered collections in which every element has a certain position. This position depends on the time and place of the insertion, but it is independent of the value of the element. For example, if you put six elements into a collection by appending each element at the end of the actual collection, these elements are in the exact order in which you put them. The STL contains three predefined sequence container classes: vector, deque, and list.
Associative containers are sorted collections in which the actual position of an element depends on its value due to a certain sorting criterion. If you put six elements into a collection, their order depends only on their value. The order of insertion doesn't matter. The STL contains four predefined associative container classes: set, multiset, map, and multimap.
An associative container can be considered a special kind of sequence container because sorted collections are ordered according to a sorting criterion. You might expect this especially if you have used other libraries of collection classes like those in Smalltalk or the NIHCL,[1] in which sorted collections are derived from ordered collections. However, note that the STL collection types are completely distinct from each other. They have different implementations that are not derived from each other.
The automatic sorting of elements in associative containers does not mean that those containers are especially designed for sorting elements. You can also sort the elements of a sequence container. The key advantage of automatic sorting is better performance when you search elements. In particular, you can always use a binary search, which results in logarithmic complexity rather than linear complexity. For example, this means that for a search in a collection of 1,000 elements you need, on average, only 10 instead of 500 comparisons (see Section 2.3). Thus, automatic sorting is only a (useful) "side effect" of the implementation of an associative container, designed to enable better performance.
The following subsections discuss the different container classes in detail. Among other aspects, they describe how containers are typically implemented. Strictly speaking, the particular implementation of any container is not defined inside the C++ standard library. However, the behavior and complexity specified by the standard do not leave much room for variation. So, in practice, the implementations differ only in minor details. Chapter 6 covers the exact behavior of the container classes. It describes their common and individual abilities, and member functions in detail.
The following sequence containers are predefined in the STL:
Vectors
Deques
Lists
In addition you can use strings and ordinary arrays as a (kind of) sequence container.
A vector manages its elements in a dynamic array. It enables random access, which means you can access each element directly with the corresponding index. Appending and removing elements at the end of the array is very fast.[2] However, inserting an element in the middle or at the beginning of the array takes time because all the following elements have to be moved to make room for it while maintaining the order.
The following example defines a vector for integer values, inserts six elements, and prints the elements of the vector:
// stl/vector1.cpp #include <iostream> #include <vector> using namespace std; int main() { vector<int> coll; //vector container for integer elements // append elements with values 1 to 6 for (int i=1; i<=6; ++i) { coll.push_back(i); } //print all elements followed by a space for (int i=0; i<coll.size( ); ++i) { cout << coll[i] << ' '; } cout << endl; }
With
#include <vector>
the header file for vectors is included.
The declaration
vector<int> coll;
creates a vector for elements of type int. The vector is not initialized by any value, so the default constructor creates it as an empty collection.
The push_back() function appends an element to the container:
coll.push_back(i);
This member function is provided for all sequence containers.
The size() member function returns the number of elements of a container:
for (int i=0; i<coll.size(); ++i) {
...
}
This function is provided for any container class.
By using the subscript operator [], you can access a single element of a vector:
cout << coll[i] << ' ';
Here the elements are written to the standard output, so the output of the whole program is as follows:
1 2 3 4 5 6
The term deque (it rhymes with "check" [3]) is an abbreviation for "double-ended queue." It is a dynamic array that is implemented so that it can grow in both directions. Thus, inserting elements at the end and at the beginning is fast. However, inserting elements in the middle takes time because elements must be moved.
The following example declares a deque for floating-point values, inserts elements from 1.1 to 6.6 at the front of the container, and prints all elements of the deque:
// stl/deque1.cpp #include <iostream> #include <deque> using namespace std; int main() { deque<float> coll; //deque container for floating-point elements //insert elements from 1.1 to 6.6 each at the front for (int i=1; i<=6; ++i) { coll.push_front(i*1. 1); //insert at the front } //print all elements followed by a space for (int i=0; i<coll.size(); ++i) { cout << coll[i] << ' '; } cout << endl; }
In this example, with
#include <deque>
the header file for deques is included.
The declaration
deque<float> coll;
creates an empty collection of floating-point values.
The push_front() function is used to insert elements:
coll.push_front(i*1.1);
push_front() inserts an element at the front of the collection. Note that this kind of insertion results in a reverse order of the elements because each element gets inserted in front of the previous inserted elements. Thus, the output of the program is as follows:
6.6 5.5 4.4 3.3 2.2 1.1
You could also insert elements in a deque by using the push_back() member function. The push_front() function, however, is not provided for vectors because it would have a bad runtime for vectors (if you insert an element at the front of a vector, all elements have to be moved). Usually, the STL containers provide only those special member functions that in general have "good" timing ("good" timing normally means constant or logarithmic complexity). This prevents a programmer from calling a function that might cause bad performance.
A list is implemented as a doubly linked list of elements. This means each element in a list has its own segment of memory and refers to its predecessor and its successor. Lists do not provide random access. For example, to access the tenth element, you must navigate the first nine elements by following the chain of their links. However, a step to the next or previous element is possible in constant time. Thus, the general access to an arbitrary element takes linear time (the average distance is proportional to the number of elements). This is a lot worse than the amortized constant time provided by vectors and deques.
The advantage of a list is that the insertion or removal of an element is fast at any position. Only the links must be changed. This implies that moving an element in the middle of a list is very fast compared with moving an element in a vector or a deque.
The following example creates an empty list of characters, inserts all characters from 'a' to 'z', and prints all elements by using a loop that actually prints and removes the first element of the collection:
// stl/list1.cpp #include <iostream> #include <list> using namespace std; int main() { list<char> coll; //list container for character elements // append elements from 'a' to 'z' for (char c='a'; c<= ' z '; ++c) { coll.push_back(c); } /* print all elements * - while there are elements * - print and remove the first element */ while (! coll.empty()) { cout << coll.front() << ' '; coll.pop_front(); } cout << endl; }
As usual, the header file for lists, <list>, is used to define a collection of type list for character values:
list<char> coll;
The empty() member function returns whether the container has no elements. The loop continues as long as it returns true (that is, the container contains elements):
while (! coll.empty()) {
...
}
Inside the loop, the front() member function returns the actual first element:
cout << coll.front() << ' ';
The pop_front() function removes the first element:
coll.pop_front();
Note that pop_front() does not return the element it removed. Thus, you can't combine the previous two statements into one.
The output of the program depends on the actual character set. For the ASCII character set, it is as follows [4]:
a b c d e f g h i j k l m n o p q r s t u v w x y z
Of course it is very strange to "print" the elements of a list by a loop that outputs and removes the actual first element. Usually, you would iterate over all elements. However, direct element access by using operator [] is not provided for lists. This is because lists don't provide random access, and thus using operator [] would cause bad performance. There is another way to loop over the elements and print them by using iterators. After their introduction I will give an example (if you can't wait, go to page 84).
You can also use strings as STL containers. By strings I mean objects of the C++ string classes (basic_string<>, string, and wstring), which are introduced in Chapter 11). Strings are similar to vectors except that their elements are characters. Section 11.2.13, provides details.
Another kind of container is a type of the core C and C++ language rather than a class: an ordinary array that has static or dynamic size. However, ordinary arrays are not STL containers because they don't provide member functions such as size() and empty(). Nevertheless, the STL's design allows you to call algorithms for these ordinary arrays. This is especially useful when you process static arrays of values as an initializer list.
The usage of ordinary arrays is nothing new. What is new is using algorithms for them. This is explained in Section 6.7.2.
Note that in C++ it is no longer necessary to program dynamic arrays directly. Vectors provide all properties of dynamic arrays with a safer and more convenient interface. See Section 6.2.3, for details.
Associative containers sort their elements automatically according to a certain ordering criterion. This criterion takes the form of a function that compares either the value or a special key that is defined for the value. By default, the containers compare the elements or the keys with operator <. However, you can supply your own comparison function to define another ordering criterion.
Associative containers are typically implemented as binary trees. Thus, every element (every node) has one parent and two children. All ancestors to the left have lesser values; all ancestors to the right have greater values. The associative containers differ in the kind of elements they support and how they handle duplicates.
The following associative containers are predefined in the STL. Because you need iterators to access their elements, I do not provide examples until page 87, where I discuss iterators.
Sets
A set is a collection in which elements are sorted according to their own values. Each element may occur only once, thus duplicates are not allowed.
Multisets
A multiset is the same as a set except that duplicates are allowed. Thus, a multiset may contain multiple elements that have the same value.
Maps
A map contains elements that are key/value pairs. Each element has a key that is the basis for the sorting criterion and a value. Each key may occur only once, thus duplicate keys are not allowed. A map can also be used as an associative array, which is an array that has an arbitrary index type (see page 91 for details).
Multimaps
A multimap is the same as a map except that duplicates are allowed. Thus, a multimap may contain multiple elements that have the same key. A multimap can also be used as dictionary. See page 209 for an example.
All of these associative container classes have an optional template argument for the sorting criterion. The default sorting criterion is the operator <. The sorting criterion is also used as the test for equality; that is, two elements are equal if neither is less than the other.
You can consider a set as a special kind of map, in which the value is identical to the key. In fact, all of these associative container types are usually implemented by using the same basic implementation of a binary tree.
In addition to the fundamental container classes, the C++ standard library provides special predefined container adapters that meet special needs. These are implemented by using the fundamental containers classes. The predefined container adapters are as follows:
Stacks
The name says it all. A stack is a container that manages its elements by the LIFO (last-in-first-out) policy.
Queues
A queue is a container that manages its elements by the FIFO (first-in-first-out) policy. That is, it is an ordinary buffer.
Priority Queues
A priority queue is a container in which the elements may have different priorities. The priority is based on a sorting criterion that the programmer may provide (by default, operator < is used). A priority queue is, in effect, a buffer in which the next element is always the element that has the highest priority inside the queue. If more than one element has the highest priority, the order of these elements is undefined.
Container adapters are historically part of the STL. However, from a programmer's view point, they are just special containers that use the general framework of the containers, iterators, and algorithms provided by the STL. Therefore, container adapters are described apart from the STL in Chapter 10.
An iterator is an object that can "iterate" (navigate) over elements. These elements may be all or part of the elements of a STL container. An iterator represents a certain position in a container. The following fundamental operations define the behavior of an iterator:
Operator *
Returns the element of the actual position. If the elements have members, you can use operator -> to access those members directly from the iterator.[5]
Operator ++
Lets the iterator step forward to the next element. Most iterators also allow stepping backward by using operator - -.
Operators == and !=
Return whether two iterators represent the same position.
Operator =
Assigns an iterator (the position of the element to which it refers).
These operations are exactly the interface of ordinary pointers in C and C++ when they are used to iterate over the elements of an array. The difference is that iterators may be smart pointers — pointers that iterate over more complicated data structures of containers. The internal behavior of iterators depends on the data structure over which they iterate. Hence, each container type supplies its own kind of iterator. In fact, each container class defines its iterator type as a nested class. As a result, iterators share the same interface but have different types. This leads directly to the concept of generic programming: Operations use the same interface but different types, so you can use templates to formulate generic operations that work with arbitrary types that satisfy the interface.
All container classes provide the same basic member functions that enable them to use iterators to navigate over their elements. The most important of these functions are as follows:
begin()
Returns an iterator that represents the beginning of the elements in the container. The beginning is the position of the first element (if any).
end()
Returns an iterator that represents the end of the elements in the container. The end is the position behind the last element. Such an iterator is also called a past-the-end iterator.
Thus, begin() and end() define a half-open range that includes the first element but excludes the last (Figure 5.3). A half-open range has two advantages:
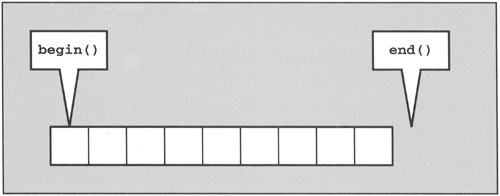
You have a simple end criterion for loops that iterate over the elements: They simply continue as long as end() is not reached.
It avoids special handling for empty ranges. For empty ranges, begin() is equal to end().
Here is an example demonstrating the use of iterators. It prints all elements of a list container (it is the promised enhanced version of the first list example).
// stl/list2.cpp #include <iostream> #include <list> using namespace std; int main() { list<char> coll; //list container for character elements // append elements from 'a' to 'z' for (char c='a'; c<='z'; ++c) { coll.push_back(c); } /*print all elements * - iterate over all elements */ list<char>::const_iterator pos; for (pos = coll.begin(); pos != coll.end(); ++pos) { cout << *pos << ' ' ; } cout << endl; }
After the list is created and filled with the characters 'a' through 'z', all elements are printed within a for loop:
list<char>::const_iterator pos;
for (pos = coll.begin(); pos != coll.end(); ++pos) {
cout << *pos << ' ';
}
The iterator pos is declared just before the loop. Its type is the iterator type for constant element access of its container class:
list<char>::const_iterator pos;
Every container defines two iterator types:
container::iterator
is provided to iterate over elements in read/write mode.
container: : const_iterator
is provided to iterate over elements in read-only mode.
For example, in class list the definitions might look like the following:
namespace std {
template <class T>
class list {
public:
typedef ... iterator;
typedef ... const_iterator;
...
};
}
The exact type of iterator and const_iterator is implementation defined.
Inside the for loop, the iterator pos first gets initialized with the position of the first element:
pos = coll.begin()
The loop continues as long as pos has not reached the end of the container elements:
pos != coll.end()
Here, pos is compared with the past-the-end iterator. While the loop runs the increment operator, ++pos navigates the iterator pos to the next element.
All in all, pos iterates from the first element, element-by-element, until it reaches the end (Figure 5.4). If the container has no elements, the loop does not run because coll.begin() would equal coll.end().
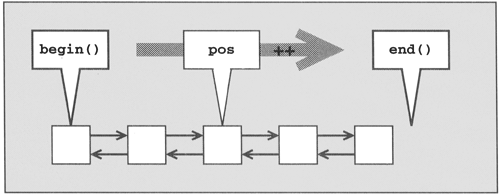
In the body of the loop, the expression *pos represents the actual element. In this example, it is written followed by a space character. You can't modify the elements because a const_iterator is used. Thus, from the iterator's point of view the elements are constant. However, if you use a nonconstant iterator and the type of the elements is nonconstant, you can change the values. For example:
//make all characters in the list uppercase
list<char>::iterator pos;
for (pos = coll.begin(); pos != coll.end(); ++pos) {
*pos = toupper(*pos);
}
Note that the preincrement operator (prefix ++) is used here. This is because it might have better performance than the postincrement operator. The latter involves a temporary object because it must return the old position of the iterator. For this reason, it generally is best to prefer ++pos over pos++. Thus, you should avoid the following version:
for (pos = coll.begin(); pos != coll.end(); pos++) {
^^^^^ // OK, but slower
...
}
For this reason, I recommend using the preincrement and pre-decrement operators in general.
The iterator loop in the previous example could be used for any container. You only have to adjust the iterator type. Now you can print elements of associative containers. The following are some examples of the use of associative containers.
The first example shows how to insert elements into a set and to use iterators to print them:
// stl/set1.cpp #include <iostream> #include <set> int main() { //type of the collection typedef std::set<int> IntSet; IntSet coll; //set container for int values /* insert elements from 1 to 6 in arbitray order *- value 1 gets inserted twice */ coll.insert(3); coll.insert(1); coll.insert(5); coll.insert(4); coll.insert(1); coll.insert(6); coll.insert(2); /* print all elements *- iterate over all elements */ IntSet::const_iterator pos; for (pos = coll.begin(); pos != coll.end(); ++pos) { std::cout << *pos << ' '; } std::cout << std::endl; }
As usual, the include directive
#include <set>
defines all necessary types and operations of sets.
The type of the container is used in several places, so first a shorter type name gets defined:
typedef set<int> IntSet;
This statement defines type IntSet as a set for elements of type int. This type uses the default sorting criterion, which sorts the elements by using operator <. This means the elements are sorted in ascending order. To sort in descending order or use a completely different sorting criterion, you can pass it as a second template parameter. For example, the following statement defines a set type that sorts the elements in descending order[6]:
typedef set<int,greater<int> > IntSet;
greater<> is a predefined function object that is discussed in Section 5.9.2. For a sorting criterion that uses only a part of the data of an object (such as the ID) see Section 8.1.1.
All associative containers provide an insert() member function to insert a new element:
coll.insert(3); coll.insert(1); ...
The new element receives the correct position automatically according to the sorting criterion. You can't use the push_back() or push_front() functions provided for sequence containers. They make no sense here because you can't specify the position of the new element.
After all values are inserted in any order, the state of the container is as shown in Figure 5.5. The elements are sorted into the internal tree structure of the container so that the value of the left child of an element is always less (with respect to the actual sorting criterion) and the value of the right child of an element is always greater. Duplicates are not allowed in a set, so the container contains the value 1 only once.
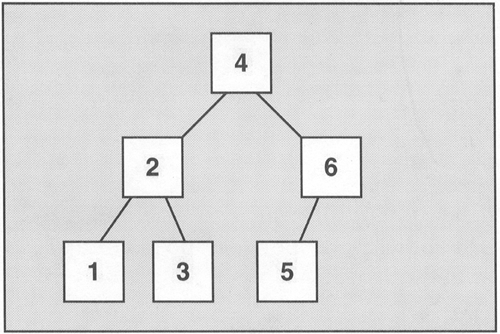
To print the elements of the container, you use the same loop as in the previous list example. An iterator iterates over all elements and prints them:
IntSet::const_iterator pos;
for (pos = coll.begin(); pos != coll.end(); ++pos) {
cout << *pos << ' ';
}
Again, because the iterator is defined by the container, it does the right thing, even if the internal structure of the container is more complicated. For example, if the iterator refers to the third element, operator ++ moves to the fourth element at the top. After the next call of operator ++ the iterator refers to the fifth element at the bottom (Figure 5.6).
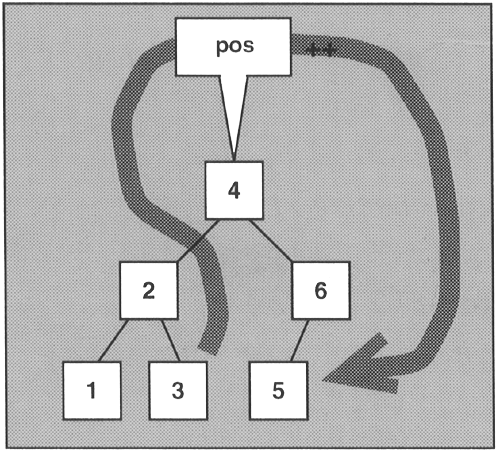
The output of the program is as follows:
1 2 3 4 5 6
If you want to use a multiset rather than a set, you need only change the type of the container (the header file remains the same):
typedef multiset<int> IntSet;
A multiset allows duplicates, so it would contain two elements that have value 1. Thus, the output of the program would change to the following:
1 1 2 3 4 5 6
The elements of maps and multimaps are key/value pairs. Thus, the declaration, the insertion, and the access to elements are a bit different. Here is an example of using a multimap:
// stl/mmap1.cpp #include <iostream> #include <map> #include <string> using namespace std; int main() { //type of the collection typedef multimap<int, string> IntStringMMap; IntStringMMap coll; //set container for int/string values //insert some elements in arbitrary order //- a value with key 1 gets inserted twice coll.insert(make_pair(5,"tagged")); coll.insert(make_pair(2,"a")); coll.insert(make_pair(1,"this")); coll.insert(make_pair(4,"of")); coll.insert(make_pair(6,"strings")); coll.insert(make_pair(1,"is")); coll.insert(make_pair(3,"multimap")); /* print all element values *- iterate over all elements *- element member second is the value */ IntStringMMap::iterator pos; for (pos = coll.begin(); pos != coll.end(); ++pos) { cout << pos->second << ' '; } cout << endl; }
The program may have the following output:
this is a multimap of tagged strings
However, because "this" and "is" have the same key, their order might be the other way around.
When you compare this example with the set example on page 87, you can see the following two differences:
The elements are key/value pairs, so you must create such a pair to insert it into the collection. The auxiliary function make_pair() is provided for this purpose. See page 203 for more details and other possible ways to insert a value.
The iterators refer to key/value pairs. Therefore, you can't just print them as a whole. Instead, you must access the members of the pair structure, which are called first and second (type pair is introduced in Section 4.1). Thus, the expression
pos->second
yields the second part of the key/value pair, which is the value of the multimap element. As with ordinary pointers, the expression is defined as an abbreviation for[7]
(*pos) .second
Similarly, the expression
pos->first
yields the first part of the key/value pair, which is the key of the multimap element.
Multimaps can also be used as dictionaries. See page 209 for an example.
In the previous example, if you replace type multimap with map you would get the output without duplicate keys (the values might still be the same). However, a collection of key/value pairs with unique keys could also be thought of as an associative array. Consider the following example:
// stl/map1.cpp #include <iostream> #include <map> #include <string> using namespace std; int main() { /* type of the container: * - map: elements key/value pairs * - string: keys have type string * - float: values have type float */ typedef map<string,float> StringFloatMap; StringFloatMap coll; //insert some elements into the collection coll["VAT"] = 0.15; coll["Pi"] = 3.1415; coll["an arbitrary number"] = 4983.223; coll["Null"] = 0; /*print all elements * - iterate over all elements * - element member first is the key * - element member second is the value */ StringFloatMap::iterator pos; for (pos = coll.begin(); pos != coll.end(); ++pos) { cout << "key: \"" << pos->first << "\" " << "value: " << pos->second << endl; } }
The declaration of the container type must specify both the type of the key and the type of the value:
typedef map<string,float> StringFloatMap;
Maps enable you to insert elements by using the subscript operator [ ]:
coll["VAT"] = 0.15; coll["Pi"] = 3.1415; coll["an arbitrary number"] = 4983.223; coll["Null"] = 0;
Here, the index is used as the key and may have any type. This is the interface of an associative array. An associative array is an array in which the index may be of an arbitrary type.
Note that the subscript operator behaves differently than the usual subscript operator for arrays: Not having an element for an index is not an error. A new index (or key) is taken as a reason to create and to insert a new element of the map that has the index as the key. Thus, you can't have a wrong index. Therefore, in this example in the statement
coll["Null"] = 0;
the expression
coll["Null"]
creates a new element that has the key "Null". The assignment operator assigns 0 (which gets converted into float) as the value. Section 6.6.3, discusses maps as associative arrays in more detail.
You can't use the subscript operator for multimaps. Multimaps allow multiple elements that have the same key, so the subscript operator makes no sense because it can handle only one value. As shown on page 90, you must create key/value pairs to insert elements into a multimap. You can do the same with maps. See page 202 for details.
Similar to multimaps, for maps to access the key and the value of an element you have to use the first and second members of the pair structure. The output of the program is as follows:
key: "Null" value: 0 key: "Pi" value: 3.1415 key: "VAT" value: 0.15 key: "an arbitrary number" value: 4983.22
Iterators can have capabilities in addition to their fundamental operations. The additional abilities depend on the internal structure of the container type. As usual, the STL provides only those operations that have good performance. For example, if containers have random access (such as vectors or deques) their iterators are also able to perform random access operations (for example, positioning the iterator directly at the fifth element).
Iterators are subdivided into different categories that are based on their general abilities. The iterators of the predefined container classes belong to one of the following two categories:
Bidirectional iterator
As the name indicates, bidirectional iterators are able to iterate in two directions: forward, by using the increment operator, and backward, by using the decrement operator. The iterators of the container classes list, set, multiset, map, and multimap are bidirectional iterators.
Random access iterator
Random access iterators have all the properties of bidirectional iterators. In addition, they can perform random access. In particular, they provide operators for "iterator arithmetic" (in accordance with "pointer arithmetic" of an ordinary pointer). You can add and subtract offsets, process differences, and compare iterators by using relational operators such as < and >. The iterators of the container classes vector and deque, and iterators of strings are random access iterators.
Other iterator categories are discussed in Section 7.2.
To write generic code that is as independent of the container type as possible, you should not use special operations for random access iterators. For example, the following loop works with any container:
for (pos = coll.begin(); pos != coll.end(); ++pos) {
...
}
However, the following does not work with all containers:
for (pos = coll.begin() ; pos < coll.end(); ++pos) {
...
}
The only difference is the use of operator < instead of operator != in the condition of the loop. Operator < is only provided for random access iterators, so this loop does not work with lists, sets, and maps. To write generic code for arbitrary containers, you should use operator != rather than operator <. However, doing so might lead to code that is less safe. This is because you may not recognize that pos gets a position behind end() (see Section 5.11, for more details about possible errors when using the STL). It's up to you to decide which version to use. It might be a question of the context, or it might even be a question of taste.
To avoid misunderstanding, note that I am talking about "categories" and not "classes." A category only defines the abilities of iterators. The type doesn't matter. The generic concept of the STL works with pure abstraction; that is, anything that behaves like a bidirectional iterator is a bidirectional iterator.
The STL provides several standard algorithms for the processing of elements of collections. These algorithms offer general fundamental services, such as searching, sorting, copying, reordering, modifying, and numeric processing.
Algorithms are not member functions of the container classes. Instead, they are global functions that operate with iterators. This has an important advantage: Instead of each algorithm being implemented for each container type, all are implemented only once for any container type. The algorithm might even operate on elements of different container types. You can also use the algorithms for user-defined container types. All in all, this concept reduces the amount of code and increases the power and the flexibility of the library.
Note that this is not an object-oriented programming paradigm; it is a generic functional programming paradigm. Instead of data and operations being unified, as in object-oriented programming, they are separated into distinct parts that can interact via a certain interface. However, this concept also has its price: First, the usage is not intuitive. Second, some combinations of data structures and algorithms might not work. Even worse, a combination of a container type and an algorithm might be possible but not useful (for example, it may lead to bad performance). Thus, it is important to learn the concepts and the pitfalls of the STL to benefit from it without abusing it. I provide examples and more details about this throughout the rest of this chapter.
Let's start with a simple example of the use of STL algorithms. Consider the following program, which shows some algorithms and their usage:
// stl/algo1.cpp #include <iostream> #include <vector> #include <algorithm> using namespace std; int main() { vector<int> coll; vector<int>::iterator pos; //insert elements from 1 to 6 in arbitrary order coll.push_back(2); coll.push_back(5); coll.push_back(4); coll.push_back(1); coll.push_back(6); coll.push_back(3); //find and print minimum and maximum elements pos = min_element (coll.begin(), coll.end()); cout << "min: " << *pos << endl; pos = max_element (coll.begin(), coll.end()); cout << "max: " << *pos << endl; //sort all elements sort (coll.begin(), coll.end()); //find the first element with value 3 pos = find (coll.begin(), coll.end(), //range 3); //value //reverse the order of the found element with value 3 and all following elements reverse (pos, coll.end()); //print all elements for (pos=coll.begin(); pos!=coll.end(); ++pos) { cout << *pos << ' ' ; } cout << endl; }
To be able to call the algorithms, you must include the header file <algorithm>:
#include <algorithm>
The first two algorithms called are min_element() and max_element(). They are called with two parameters that define the range of the processed elements. To process all elements of a container you simply use begin() and end(). Both algorithms return an iterator for the minimum and maximum elements respectively. Thus, in the statement
pos = min_element (coll.begin(), coll.end());
the min_element() algorithm returns the position of the minimum element (if there is more than one, the algorithm returns the first). The next statement prints that element:
cout << "min: " << *pos << endl;
Of course, you could do both in one statement:
cout << *max_element(coll.begin(), coll.end()) << endl;
The next algorithm called is sort(). As the name indicates, it sorts the elements of the range defined by the two arguments. As usual, you could pass an optional sorting criterion. The default sorting criterion is operator <. Thus, in this example all elements of the container are sorted in ascending order:
sort (coll.begin(), coll.end());
So afterward, the vector contains the elements in this order:
1 2 3 4 5 6
The find() algorithm searches for a value inside the given range. In this example, it searches the first element that is equal to the value 3 in the whole container:
pos = find (coll.begin(), coll.end(), //range 3); //value
If the find() algorithm is successful, it returns the iterator position of the element found. If it fails, it returns the end of the range, the past-the-end iterator, which is passed as the second argument. In this example, the value 3 is found as the third element, so afterward pos refers to the third element of coll.
The last algorithm called in the example is reverse(), which reverses the elements of the passed range. Here the third element that was found by the find() algorithms and the past-the-end iterator are passed as arguments:
reverse (pos, coll.end());
This call reverses the order of the third element up to the last one. The output of the program is as follows:
min: 1 max: 6 1 2 6 5 4 3
All algorithms process one or more ranges of elements. Such a range might, but is not required to, embrace all elements of a container. Therefore, to be able to handle subsets of container elements, you pass the beginning and the end of the range as two separate arguments rather than the whole collection as one argument.
This interface is flexible but dangerous. The caller must ensure that the first and second arguments define a valid range. This is the case if the end of the range is reachable from the beginning by iterating through the elements. This means, it is up to the programmer to ensure that both iterators belong to the same container and that the beginning is not behind the end. If this is not the case, the behavior is undefined and endless loops or forbidden memory access may result. In this respect, iterators are just as unsafe as ordinary pointers. But note that undefined behavior also means that an implementation of the STL is free to find such kinds of errors and handle them accordingly. The following paragraphs show that ensuring that ranges are valid is not always as easy as it sounds. See Section 5.11, for more details about the pitfalls and safe versions of the STL.
Every algorithm processes half-open ranges. Thus, a range is defined so that it includes the position used as the beginning of the range but excludes the position used as the end. This concept is often described by using the traditional mathematical notations for half-open ranges:
[begin,end)
or
[begin,end[
I use the first alternative in this book.
The half-open range concept has the advantages that were described on page 84 (it is simple and avoids special handling for empty collections). However, it also has some disadvantages. Consider the following example:
// stl/find1.cpp #include <iostream> #include <list> #include <algorithm> using namespace std; int main() { list<int> coll; list<int>::iterator pos; //insert elements from 20 to 40 for (int i=20; i<=40; ++i) { coll.push_back(i); } /*find position of element with value 3 * - there is none, so pos gets coll.end() */ pos = find (coll .begin() , coll.end(), //range 3); //value /*reverse the order of elements between found element and the end * - because pos is coll.end() it reverses an empty range */ reverse (pos, coll.end()); //find positions of values 25 and 35 list<int>::iterator pos25, pos35; pos25 = find (coll.begin(), coll.end(), //range 25); //value pos35 = find (coll.begin(), coll.end(), //range 35); //value /*print the maximum of the corresponding range * - note: including pos25 but excluding pos35 */ cout << "max: " << *max_element (pos25, pos35) << endl; //process the elements including the last position cout << "max: " << *max_element (pos25, ++pos35) << endl; }
In this example, the collection is initialized with integral values from 20 to 40. When the search for an element with the value 3 fails, find() returns the end of the processed range (coll.end() in this example) and assigns it to pos. Using that return value as the beginning of the range in the following call of reverse() poses no problem because it results in the following call:
reverse (coll.end(), coll.end());
This is simply a call to reverse an empty range. Thus, it is an operation that has no effect (a so-called "no-op").
However, if find() is used to find the first and the last elements of a subset, you should consider that passing these iterator positions as a range will exclude the last element. So, the first call of max_element()
max_element (pos25, pos35)
finds 34 and not 35:
max: 34
To process the last element, you have to pass the position that is one past the last element:
max_element (pos25, ++pos35)
Doing this yields the correct result:
max: 35
Note that this example uses a list as the container. Thus, you must use operator ++ to get the position that is behind pos35. If you have random access iterators, as with vectors and deques, you also could use the expression pos35 + 1. This is because random access iterators allow "iterator arithmetic" (see Section 2, page 93, and Section 7.2.5, for details).
Of course, you could use pos25 and pos35 to find something in that subrange. Again, to search including pos35 you have to pass the position after pos35. For example:
//increment pos35 to search with its value included ++pos35; pos30 = find(pos25,pos35, //range 30); //value if (pos30 == pos35) { cout << "30 is in NOT the subrange" << endl; } else { cout << "30 is in the subrange" << endl; }
All the examples in this section work only because you know that pos25 is in front of pos35. Otherwise, [pos25,pos35) would not be a valid range. If you are not sure which element is in front, things are getting more complicated and undefined behavior may occur.
Suppose you don't know whether the element that has value 25 is in front of the element that has value 35. It might even be possible that one or both values are not present. By using random access iterators, you can call operator < to check this:
if (pos25 < pos35) {
//only [pos25,pos35) is valid
...
}
else if (pos35 < pos25) {
//only [pos35,pos25) is valid
...
}
else {
//both are equal, so both must be end()
...
}
However, without random access iterators you have no simple, fast way to find out which iterator is in front. You can only search for one iterator in the range of the beginning to the other iterator or in the range of the other iterator to the end. In this case, you should change your algorithm as follows: Instead of searching for both values in the whole source range, you should try to find out, while searching for them, which value comes first. For example:
pos25 = find (coll.begin(), coll.end(), //range 25); //value pos35 = find (coll.begin(), pos25, //range 35); //value if (pos35 != pos25) { /*pos35 is in front of pos25 *so, only [pos35,pos25) is valid */ ... } else { pos35 = find (pos25, coll.end(), //range 35); //value if (pos35 != pos25) { /*pos25 is in front of pos35 *so, only [pos25,pos35) is valid */ ... } else { // both are equal, so both must be end() ... } }
In contrast to the previous version, here you don't search for pos35 in the full range of all elements of coll. Instead, you first search for it from the beginning to pos25. Then, if it's not found, you search for it in the part that contains the remaining elements after pos25. As a result you know which iterator position comes first and which subrange is valid.
This implementation is not very efficient. A more efficient way to find the first element that either has value 25 or value 35 is to search exactly for that. You could do this by using some abilities of the STL that are not introduced yet as follows:
pos = find_if (coll.begin(), coll.end(), //range compose_f_gx_hx(logical_or<bool>(), //criterion bind2nd(equal_to<int>(), 25), bind2nd(equal_to<int>(), 35))); switch (*pos) { case 25: //element with value 25 comes first pos25 = pos; pos35 = find (++pos, coll.end(), //range 35); //value ... break; case 35: //element with value 35 comes first pos35 = pos; pos25 = find (++pos, coll.end(), //range 25); //value ... break; default: //no element with value 25 or 35 found ... break; }
Here, a special expression is used as a sorting criterion that allows a search of the first element that has either value 25 or value 35. The expression is a combination of several predefined function objects, which are introduced in Section 5.9.2, and Section 8.2, and a supplementary function object compose_f_gx_hx, which is introduced in Section 8.3.1.
Several algorithms process more than one range. In this case you usually must define both the beginning and the end only for the first range. For all other ranges you need to pass only their beginnings. The ends of the other ranges follow from the number of elements of the first range. For example, the following call of equal() compares all elements of the collection coll1 element-by-element with the elements of coll2 beginning with its first element:
if (equal (coll1.begin(), coll1.end(),
coll2.begin())) {
...
}
Thus, the number of elements of coll2 that are compared with the elements of coll1 is specified indirectly by the number of elements in coll1.
This leads to an important consequence: When you call algorithms for multiple ranges, make sure the second and additional ranges have at least as many elements as the first range. In particular, make sure that destination ranges are big enough for algorithms that write to collections!
Consider the following program:
// stl/copy1.cpp #include <iostream> #include <vector> #include <list> #include <algorithm> using namespace std; int main() { list<int> coll1; vector<int> coll2; //insert elements from 1 to 9 for (int i=1; i<=9; ++i) { coll1.push_back(i); } //RUNTIME ERROR: // - overwrites nonexisting elements in the destination copy (coll1 .begin(), coll1.end(), //source coll2.begin()); //destination ...... }
Here, the copy() algorithm is called. It simply copies all elements of the first range into the destination range. As usual, for the first range, the beginning and the end are defined, whereas for the second range, only the beginning is specified. However, the algorithm overwrites rather than inserts. So, the algorithm requires that the destination has enough elements to be overwritten. If there is not enough room, as in this case, the result is undefined behavior. In practice, this often means that you overwrite whatever comes after the coll2.end(). If you're in luck, you'll get a crash; at least then you'll know that you did something wrong. However, you can force your luck by using a safe version of the STL for which the undefined behavior is defined as leading to a certain error handling procedure (see Section 5.11.1).
To avoid these errors, you can (1) ensure that the destination has enough elements on entry, or (2) use insert iterators. Insert iterators are covered in Section 5.5.1. I'll first explain how to modify the destination so that it is big enough on entry.
To make the destination big enough, you must either create it with the correct size or change its size explicitly. Both alternatives apply only to sequence containers (vectors, deques, and lists). This is not really a problem because associative containers cannot be used as a destination for purposes for overwriting algorithms (Section 5.6.2, explains why). The following program shows how to increase the size of containers:
// stl/copy2.cpp #include <iostream> #include <vector> #include <list> #include <deque> #include <algorithm> using namespace std; int main() { list<int> coll1; vector<int> coll2; //insert elements from 1 to 9 for (int i=1; i<=9; ++i) { coll1.push_back(i); } //resize destination to have enough room for the overwriting algorithm coll2.resize (coll1. size()); /*copy elements from first into second collection *- overwrites existing elements in destination */ copy (coll1.begin(), coll1.end(), //source coll2.begin()); //destination /*create third collection with enough room *- initial size is passed as parameter */ deque<int> coll3(coll1 size()); //copy elements from first into third collection copy (coll1.begin(), coll1.end(), //source coll3.begin()); //destination }
Here, resize() is used to change the number of elements in the existing container coll2:
coll2.resize (coll1.size());
coll3 is initialized with a special initial size so that it has enough room for all elements of coll1:
deque<int> coll3(coll1.size());
Note that both resizing and initializing the size create new elements. These elements are initialized by their default constructor because no arguments are passed to them. You can pass an additional argument both for the constructor and for resize() to initialize the new elements.
Iterators are pure abstractions: Anything that behaves like an iterator is an iterator. For this reason, you can write classes that have the interface of iterators but do something (completely) different. The C++ standard library provides several predefined special iterators: iterator adapters. They are more than auxiliary classes; they give the whole concept a lot more power.
The following subsections introduce three iterator adapters:
Insert iterators
Stream iterators
Reverse iterators
Section 7.4, will cover them in detail.
The first example of iterator adapters are insert iterators, or inserters. Inserters are used to let algorithms operate in insert mode rather than in overwrite mode. In particular, they solve the problem of algorithms that write to a destination that does not have enough room: They let the destination grow accordingly.
Insert iterators redefine their interface internally as follows:
If you assign a value to their actual element, they insert that value into the collection to which they belong. Three different insert iterators have different abilities with regard to where the elements are inserted — at the front, at the end, or at a given position.
A call to step forward is a no-op.
Consider the following example:
// stl/copy3.cpp #include <iostream> #include <vector> #include <list> #include <deque> #include <set> #include <algorithm> using namespace std; int main() { list<int> coll1; //insert elements from 1 to 9 into the first collection for (int i=1; i<=9; ++i) { coll1.push_back(i); } // copy the elements of coll1 into coll2 by appending them vector<int> coll2; copy (coll1.begin(), coll1.end(), //source back_inserter(coll2)); //destination //copy the elements of coll1 into coll3 by inserting them at the front // - reverses the order of the elements deque<int> coll3; copy (coll1.begin(), coll1.end(), //source front_inserter(coll3)); //destination //copy elements of coll1 into coll4 // - only inserter that works for associative collections set<int> coll4; copy (coll1.begin(), coll1.end(), //source inserter(coll4,coll4.begin())); //destination }
This example uses all three predefined insert iterators:
Back inserters
Back inserters insert the elements at the back of their container (appends them) by calling push_back(). For example, with the following statement, all elements of coll1 are appended into coll2:
copy (coll1.begin(), coll1.end(), //source back_inserter(coll2)); //destination
Of course, back inserters can be used only for containers that provide push_back() as a member function. In the C++ standard library, these containers are vector, deque, and list.
Front inserters
Front inserters insert the elements at the front of their container by calling push_front(). For example, with the following statement, all elements of coll1 are inserted into coll3:
copy (coll1.begin(), coll1.end(), //source front_inserter(coll3)) ; //destination
Note that this kind of insertion reverses the order of the inserted elements. If you insert 1 at the front and then 2 at the front, the 1 is after the 2.
Front inserters can be used only for containers that provide push_front() as a member function. In the C++ standard library, these containers are deque and list.
General inserters
A general inserter, also called simply an inserter, inserts elements directly in front of the position that is passed as the second argument of its initialization. It calls the insert() member function with the new value and the new position as arguments. Note that all predefined containers have such an insert() member function. This is the only predefined inserter for associative containers.
But wait a moment. I said that you can't specify the position of a new element in an associative container because the positions of the elements depend on their values. The solution is simple: For associative containers, the position is taken as a hint to start the search for the correct position. If the position is not correct, however, the timing may be worse than if there was no hint. Section 7.5.2, describes a user-defined inserter that is more useful for associative containers.
Table 5.1 lists the functionality of insert iterators. Additional details are described in Section 7.4.2.
| Expression | Kind of Inserter |
|---|---|
| back_inserter (container) | Appends in the same order by using push_back() |
| front_inserter (container) | Inserts at the front in reverse order by using push_front() |
| inserter (container ,pos) | Inserts at pos (in the same order) by using insert() |
Another very helpful kind of iterator adapter is a stream iterator. Stream iterators are iterators that read from and write to a stream. [8] Thus, they provide an abstraction that lets the input from the keyboard behave as a collection, from which you can read. Similarly you can redirect the output of an algorithm directly into a file or onto the screen.
Consider the following example. It is a typical example of the power of the whole STL. Compared with ordinary C or C++, it does a lot of complex processing by using only a few statements:
// stl/ioiter1.cpp #include <iostream> #include <vector> #include <string> #include <algorithm> using namespace std; int main() { vector<string> coll; /*read all words from the standard input * - source: all strings until end-of-file (or error) * - destination: coll (inserting) */ copy (istream_iterator<string>(cin), //start of source istream_iterator<string>(), //end of source back_inserter(coll)); //destination //sort elements sort (coll.begin(), coll.end()); /*print all elements without duplicates * - source: coll * - destination: standard output (with newline between elements) */ unique_copy (coll.begin(), coll.end(), //source ostream_iterator<string> (cout, "\n")); //destination }
The program has only three statements that read all words from the standard input and print a sorted list of them. Let's consider the three statements step-by-step. In the statement
copy (istream_iterator<string>(cin),
istream_iterator<string>(),
back_inserter(coll));
two input stream iterators are used:
The expression
istream_iterator<string>(cin)
creates a stream iterator that reads from the standard input stream cin.[9] The template argument string specifies that the stream iterator reads elements of this type (string types are covered in Chapter 11). These elements are read with the usual input operator >>. Thus, each time the algorithm wants to process the next element, the istream iterator transforms that desire into a call of
cin >> string
The input operator for strings usually reads one word separated by whitespaces (see page 492), so the algorithm reads word-by-word.
The expression
istream_iterator<string>()
calls the default constructor of istream iterators that creates an end-of-stream iterator. It represents a stream from which you can no longer read.
As usual, the copy() algorithm operates as long as the (incremented) first argument differs from the second argument. The end-of-stream iterator is used as the end of the range, so the algorithm reads all strings from cin until it can no longer read any more (due to end-of-stream or an error). To summarize, the source of the algorithm is "all words read from cin." These words are copied by inserting them into coll with the help of a back inserter.
The sort() algorithm sorts all elements:
sort (coll.begin(), coll.end());
Lastly, the statement
unique_copy (coll.begin(), coll.end(),
ostream_iterator<string>(cout,"\n"));
copies all elements from the collection into the destination cout. During the process, the unique_copy() algorithm eliminates adjacent duplicate values. The expression
ostream_iterator<string>(cout,"\n")
creates an output stream iterator that writes strings to cout by calling operator >> for each element. The second argument behind cout serves as a separator between the elements. It is optional. In this example, it is a newline, so every element is written on a separate line.
All components of the program are templates, so you can change the program easily to sort other value types, such as integers or more complex objects. Section 7.4.3, explains more and gives more examples about iostream iterators.
In this example, one declaration and three statements were used to sort all words from standard input. However, you could do the same by using only one declaration and one statement. See page 228 for an example.
The third kind of predefined iterator adapters are reverse iterators. Reverse iterators operate in reverse. They switch the call of an increment operator internally into a call of the decrement operator, and vice versa. All containers can create reverse iterators via their member functions rbegin() and rend(). Consider the following example:
// stl/riter1.cpp #include <iostream> #include <vector> #include <algorithm> using namespace std; int main() { vector<int> coll; //insert elements from 1 to 9 for (int i=1; i<=9; ++i) { coll.push_back(i); } //print all element in reverse order copy (coll.rbegin(), coll.rend(), //source ostream_iterator<int> (cout," ")); //destination cout << endl; }
The expression
coll.rbegin()
returns a reverse iterator for coll. This iterator may be used as the beginning of a reverse iteration over the elements of the collection. Its position is the last element of the collection. Thus, the expression
*coll.rbegin()
returns the value of the last element.
Accordingly, the expression
coll.rend()
returns a reverse iterator for coll that may be used as the end of a reverse iteration. As usual for ranges, its position is past the end of the range, but from the opposite direction; that is, it is the position before the first element in the collection.
The expression
*coll.rend()
is as undefined as is
*coll.end()
You should never use operator * (or operator ->) for a position that does not represent a valid element.
The advantage of using reverse iterators is that all algorithms are able to operate in the opposite direction without special code. A step to the next element with operator ++ is redefined into a step backward with operator --. For example, in this case, copy() iterates over the elements of coll from the last to the first element. So, the output of the program is as follows:
9 8 7 6 5 4 3 2 1
You can also switch "normal" iterators into reverse iterators, and vice versa. However, in doing so the element of an iterator changes. This and other details about reverse iterators are covered in Section 7.4.1.
Several algorithms modify destination ranges. In particular, they may remove elements. If this happens, special aspects apply. These aspects are explained in this section. They are surprising and show the price of the STL concept that separates containers and algorithms with great flexibility.
The remove() algorithm removes elements from a range. However, if you use it for all elements of a container it operates in a surprising way. Consider the following example:
// stl/remove1.cpp #include <iostream> #include <list> #include <algorithm> using namespace std; int main() { list<int> coll; //insert elements from 6 to 1 and 1 to 6 for (int i=1; i<=6; ++i) { coll.push_front(i); coll.push_back(i); } //print all elements of the collection cout << "pre: "; copy (coll.begin(), coll.end(), //source ostream_iterator<int> (cout," ")); //destination cout << endl; //remove all elements with value 3 remove (coll.begin() , coll.end(), //range 3); //value //print all elements of the collection cout << "post: "; copy (coll.begin(), coll.end(), //source ostream_iterator<int> (cout," ")); //destination cout << endl; }
Someone reading this program without deeper knowledge would expect that all elements with value 3 are removed from the collection. However, the output of the program is as follows:
pre: 6 5 4 3 2 1 1 2 3 4 5 6 post: 6 5 4 2 1 1 2 4 5 6 5 6
Thus, remove() did not change the number of elements in the collection for which it was called.
The end() member function returns the old end, whereas size() returns the old number of elements. However, something has changed: The elements changed their order as if the elements were removed. Each element with value 3 was overwritten by the following elements (Figure 5.7). At the end of the collection, the old elements that were not overwritten by the algorithm remain unchanged. Logically, these elements no longer belong to the collection.
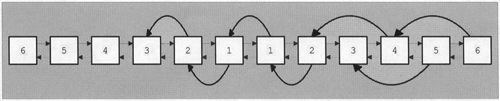
However, the algorithm does return the new end. By using it, you can access the resulting range, reduce the size of the collection, or process the number of removed elements. Consider the following modified version of the example:
// stl/remove2.cpp #include <iostream> #include <list> #include <algorithm> using namespace std; int main() { list<int> coll; //insert elements from 6 to 1 and 1 to 6 for (int i=1; i<=6; ++i) { coll.push_front(i); coll.push_back(i); } //print all elements of the collection copy (coll.begin(), coll.end(), ostream_iterator<int>(cout," ")); cout << endl; //remove all elements with value 3 // - retain new end list<int>::iterator end = remove (coll.begin(), coll.end(), 3); //print resulting elements of the collection copy (coll.begin(), end, ostream_iterator<int>(cout," ")); cout << endl; //print number of resulting elements cout << "number of removed elements: " << distance(end,coll.end()) << endl; //remove "removed'' elements coll.erase (end, coll.end()); //print all elements of the modified collection copy (coll.begin(), coll.end(), ostream_iterator<int>(cout," ")); cout << endl; }
In this version, the return value of remove() is assigned to the iterator end:
list<int>::iterator end = remove (coll.begin(), coll.end(),
3);
This is the new logical end of the modified collection after the elements are "removed." You can use this return value as the new end for further operations:
copy (coll.begin(), end,
ostream_iterator<int>(cout," "));
Another possibility is to process the number of "removed" elements by processing the distance between the "logical" and the real ends of the collection:
cout << "number of removed elements: "
<< distance(end,coll.end()) << endl;
Here, a special auxiliary function for iterators, distance(), is used. It returns the distance between two iterators. If the iterators were random access iterators you could process the difference directly with operator -. However, the container is a list, so it provides only bidirectional iterators. See Section 7.3.2, for details about distance().[10]
If you really want to remove the "removed" elements, you must call an appropriate member function of the container. To do this, containers provide the erase() member function, erase() removes all elements of the range that is specified by its arguments:
coll.erase (end, coll.end());
Here is the output of the whole program:
6 5 4 3 2 1 1 2 3 4 5 6 6 5 4 2 1 1 2 4 5 6 number of removed elements: 2 6 5 4 2 1 1 2 4 5 6
If you really want to remove elements in one statement, you can call the following statement:
coll.erase (remove(coll.begin(),coll.end(),
3),
coll.end());
Why don't algorithms call erase() by themselves? Well, this question highlights the price of the flexibility of the STL. The STL separates data structures and algorithms by using iterators as the interface. However, iterators are an abstraction to represent a position in a container. In general, iterators do not know their containers. Thus, the algorithms, which use the iterators to access the elements of the container, can't call any member function for it.
This design has important consequences because it allows algorithms to operate on ranges that are different from "all elements of a container." For example, the range might be a subset of all elements of a collection. And, it might even be a container that provides no erase() member function (ordinary arrays are an example of such a container). So, to make algorithms as flexible as possible, there are good reasons not to require that iterators know their container.
Note that it is often not necessary to remove the "removed" elements. Often, it is no problem to use the returned new logical end instead of the real end of the container. In particular, you can call all algorithms with the new logical end.
Manipulation algorithms (those that remove elements as well as those that reorder or modify elements) have another problem when you try to use them with associative containers: Associative containers can't be used as a destination. The reason for this is simple: If modifying algorithms would work for associative containers, they could change the value or position of elements so that they are not sorted anymore. This would break the general rule that elements in associative containers are always sorted automatically according to their sorting criterion. So, not to compromise the sorting, every iterator for an associative container is declared as an iterator for a constant value (or key). Thus, manipulating elements of or in associative containers results in a failure at compile time. [11]
Note that this problem prevents you from calling removing algorithms for associative containers because these algorithms manipulate elements implicitly. The values of "removed" elements are overwritten by the following elements that are not removed.
Now the question arises, How does one remove elements in associative containers? Well, the answer is simple: Call their member functions! Every associative container provides member functions to remove elements. For example, you can call the member function erase() to remove elements:
// stl/remove3.cpp #include <iostream> #include <set> #include <algorithm> using namespace std; int main() { set<int> coll; //insert elements from 1 to 9 for (int i=1; i<=9; ++i) { coll.insert(i); } //print all elements of the collection copy (coll.begin(), coll.end(), ostream_iterator<int>(cout," ")); cout << endl; /*Remove all elements with value 3 * - algorithm remove() does not work * - instead member function erase() works */ int num = coll.erase(3); //print number of removed elements cout << "number of removed elements: " << num << endl; //print all elements of the modified collection copy (coll.begin(), coll.end(), ostream_iterator<int>(cout," ")); cout << endl; }
Note that containers provide different erase() member functions. Only the form that gets the value of the element(s) to remove as a single argument returns the number of removed elements. Of course, when duplicates are not allowed, the return value can only be 0 or 1 (as is the case for sets and maps).
The output of the program is as follows:
1 2 3 4 5 6 7 8 9 number of removed elements: 1 1 2 4 5 6 7 8 9
Even if you are able to use an algorithm, it might be a bad idea to do so. A container might have member functions that provide much better performance.
Calling remove() for elements of a list is a good example of this. If you call remove() for elements of a list, the algorithm doesn't know that it is operating on a list. Thus, it does what it does for any container: It reorders the elements by changing their values. If, for example, it removes the first element, all the following elements are assigned to their previous elements. This behavior contradicts the main advantage of lists — the ability to insert, move, and remove elements by modifying the links instead of the values.
To avoid bad performance, lists provide special member functions for all manipulating algorithms. You should always use them. Furthermore, these member functions really remove "removed" elements, as this example shows:
// stl/remove4.cpp #include <iostream> #include <list> #include <algorithm> using namespace std; int main() { list<int> coll; //insert elements from 6 to 1 and 1 to 6 for (int i=1; i<=6; ++i) { coll.push_front(i); coll.push_back(i); } //remove all elements with value 3 //- poor performance coll.erase (remove(coll.begin(),coll.end(), 3), coll.end()); //remove all elements with value 4 //- good performance coll.remove (4); }
You should always prefer a member function over an algorithm if good performance is the goal. The problem is, you have to know that a member function exists that has significantly better performance for a certain container. No warning or error message appears if you use the remove() algorithm for a list. However, if you prefer a member function in these cases you have to change the code when you switch to another container type. In the reference sections of algorithms (Chapter 9) I mention when a member function exists that provides better performance than an algorithm.
The STL is an extensible framework. This means you can write your own functions and algorithms to process elements of collections. Of course, these operations may also be generic. However, to declare a valid iterator in these operations, you must use the type of the container, which is different for each container type. To facilitate the writing of generic functions, each container type provides some internal type definitions. Consider the following example:
// stl/print.hpp #include <iostream> /* PRINT_ELEMENTS() * - prints optional C-string optcstr followed by * - all elements of the collection coll * - separated by spaces */ template <class T> inline void PRINT_ELEMENTS (const T& coll, const char* optcstr="") { typename T::const_iterator pos; std::cout << optcstr; for (pos=coll.begin(); pos!=coll.end(); ++pos) { std::cout << *pos << ' '; } std::cout << std::endl; }
This example defines a generic function that prints an optional string followed by all elements of the passed container. In the declaration
typename T::const_iterator pos;
pos is declared as having the iterator type of the passed container type, typename is necessary to specify that const_iterator is a type and not a value of type T (see the introduction of typename on page 11).
In addition to iterator and const_iterator, containers provide other types to facilitate the writing of generic functions. For example, they provide the type of the elements to enable the handling of temporary copies of elements. See Section 7.5.1, for details.
The optional second argument of PRINT_ELEMENTS is a string that is used as a prefix before all elements are written. Thus, by using PRINT_ELEMENTS() you could comment or introduce the output like this:
PRINT_ELEMENTS (coll, "all elements: ");
I introduced this function here because I use it often in the rest of the book to print all elements of containers by using a simple call.
To increase their flexibility and power, several algorithms allow the passing of user-defined auxiliary functions. These functions are called internally by the algorithms.
The simplest example is the for_each() algorithm. It calls a user-defined function for each element of the specified range. Consider the following example:
// stl/foreach1.cpp #include <iostream> #include <vector> #include <algorithm> using namespace std; //function that prints the passed argument void print (int elem) { cout << elem << ' ' ; } int main() { vector<int> coll; //insert elements from 1 to 9 for (int i=1; i<=9; ++i) { coll.push_back(i); } //print all elements for_each (coll.begin(), coll.end(), //range print); //operation cout << endl; }
The for_each() algorithm calls the passed print() function for every element in the range [coll.begin(),coll.end()). Thus, the output of the program is as follows:
1 2 3 4 5 6 7 8 9
Algorithms use auxiliary functions in several variants—some optional, some mandatory. In particular, you can use them to specify a search criterion, a sorting criterion, or to define a manipulation while transferring elements from one collection to another.
Here is another example program:
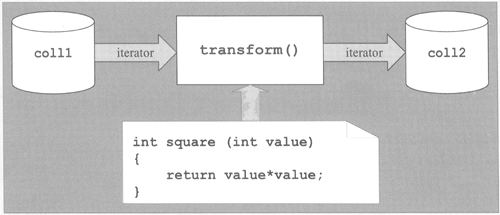
// stl/transform1.cpp #include <iostream> #include <vector> #include <set> #include <algorithm> #include "print.hpp" int square (int value) { return value*value; } int main() { std::set<int> coll1; std::vector<int> coll2; //insert elements from 1 to 9 into coll1 for (int i=1; i<=9; ++i) { coll1.insert(i); } PRINT_ELEMENTS(coll1,"initialized: "); //transform each element from coll1 to coll2 // - square transformed values std::transform (coll1.begin(),coll1.end(), //source std::back_inserter(coll2), //destination square); //operation PRINT_ELEMENTS(coll2,"squared: "); }
In this example, square() is used to square each element of coll1 while it is transformed to coll2 (Figure 5.8). The program has the following output:
initialized: 1 2 3 4 5 6 7 8 9 squared: 1 4 9 16 25 36 49 64 81
A special kind of auxiliary function for algorithms is a predicate. Predicates are functions that return a Boolean value. They are often used to specify a sorting or a search criterion. Depending on their purpose, predicates are unary or binary. Note that not every unary or binary function that returns a Boolean value is a valid predicate. The STL requires that predicates always yield the same result for the same value. This rules out functions that modify their internal state when they are called. See Section 8.1.4, for details.
Unary predicates check a specific property of a single argument. A typical example is a function that is used as a search criterion to find the first prime number:
// stl/prime1.cpp #include <iostream> #include <list> #include <algorithm> #include <cstdlib> //for abs() using namespace std; //predicate, which returns whether an integer is a prime number bool isPrime (int number) { //ignore negative sign number = abs(number); // 0 and 1 are prime numbers if (number == 0 || number == 1) { return true; } //find divisor that divides without a remainder int divisor; for (divisor = number/2; number%divisor != 0; --divisor) { ; } //if no divisor greater than 1 is found, it is a prime number return divisor == 1; } int main() { list<int> coll; //insert elements from 24 to 30 for (int i=24; i<=30; ++i) { coll.push_back(i); } //search for prime number list<int>::iterator pos; pos = find_if (coll.begin(), coll.end(), //range is Prime); //predicate if (pos != coll.end()) { //found cout << *pos << " is first prime number found" << endl; } else { //not found cout << "no prime number found" << endl; } }
In this example, the find_if() algorithm is used to search for the first element of the given range for which the passed unary predicate yields true. Here, the predicate is the isPrime() function. This function checks whether a number is a prime number. By using it, the algorithm returns the first prime number in the given range. If the algorithm does not find any element that matches the predicate, it returns the end of the range (its second argument). This is checked after the call. The collection in this example has a prime number between 24 and 30. So the output of the program is as follows:
29 is first prime number found
Binary predicates typically compare a specific property of two arguments. For example, to sort elements according to your own criterion you could provide it as a simple predicate function. This might be necessary because the elements do not provide operator < or because you wish to use a different criterion.
The following example sorts elements of a set by the first name and last name of a person:
// stl/sort1.cpp #include <iostream> #include <string> #include <deque> #include <algorithm> using namespace std; class Person { public: string firstname() const; string lastname() const; ... }; /*binary function predicate: *- returns whether a person is less than another person */ bool personSortCriterion (const Person& p1, const Person& p2) { /*a person is less than another person *- if the last name is less *- if the last name is equal and the first name is less */ return p1.lastname()<p2.1astname() || (!(p2.1astname()<p1.lastname()) && p1.firstname()<p2.firstname()); } int main() { deque<Person> coll; ... sort (coll. begin(), coll. end() , //range personSortCriterion); //sort criterion ... }
Note that you can also implement a sorting criterion as a function object. This kind of implementation has the advantage that the criterion is a type, which you could use, for example, to declare sets that use this criterion for sorting its elements. See Section 8.1.1, for such an implementation of this sorting criterion.
Functional arguments for algorithms don't have to be functions. They can be objects that behave as functions. Such an object is called a function object, or functor. Sometimes you can use a function object when an ordinary function won't work. The STL often uses function objects and provides several function objects that are very helpful.
Function objects are another example of the power of generic programming and the concept of pure abstraction. You could say that anything that behaves like a function is a function. So, if you define an object that behaves as a function, it can be used as a function.
So, what is the behavior of a function? The answer is: A functional behavior is something that you can call by using parentheses and passing arguments. For example:
function (arg1 ,arg2); //a function call
So, if you want objects to behave this way you have to make it possible to "call" them by using parentheses and passing arguments. Yes, that's possible (there are rarely things that are not possible in C++). All you have to do is define operator () with the appropriate parameter types:
class X {
public:
//define "function call" operator
return-value operator() (arguments) const;
...
};
Now you can use objects of this class to behave as a function that you can call:
X fo; ... fo(arg1, arg2); //call operator () for function object fo
The call is equivalent to:
fo.operator() (arg1,arg2); //call operator () for function object fo
The following is a complete example. This is the function object version of a previous example (see page 119) that did the same with an ordinary function:
// stl/foreach2.cpp #include <iostream> #include <vector> #include <algorithm> using namespace std; //simple function object that prints the passed argument class PrintInt { public: void operator() (int elem) const { cout << elem << ' '; } }; int main() { vector<int> coll; //insert elements from 1 to 9 for (int i=1; i<=9; ++i) { coll.push_back(i); } //print all elements for_each (coll.begin(), coll.end(), //range PrintInt()); //operation cout << endl; }
The class PrintInt defines objects for which you can call operator () with an int argument. The expression
PrintInt()
in the statement
for_each (coll.begin(), coll.end(),
PrintInt());
creates a temporary object of this class, which is passed to the for_each() algorithm as an argument. The for_each() algorithm is written like this:
namespace std {
template <class Iterator, class Operation>
Operation for_each (Iterator act, Iterator end, Operation op)
{
while (act != end) { //as long as not reached the end
op (*act); // - call op() for actual element
act++; // - move iterator to the next element
}
return op; }
}
}
for_each() uses the temporary function object op to call op(*act) for each element act. If the third parameter is an ordinary function, it simply calls it with *act as an argument. If the third parameter is a function object, it calls operator () for the function object op with *act as an argument. Thus, in this example program for_each() calls:
PrintInt::operator()(*act)
You may be wondering what all this is good for. You might even think that function objects look strange, nasty, or nonsensical. It is true that they do complicate code. However, function objects are more than functions, and they have some advantages:
Function objects are "smart functions."
Objects that behave like pointers are smart pointers. This is similarly true for objects that behave like functions: They can be "smart functions" because they may have abilities beyond operator (). Function objects may have other member functions and attributes. This means that function objects have a state. In fact, the same function, represented by a function object, may have different states at the same time. This is not possible for ordinary functions. Another advantage of function objects is that you can initialize them at runtime before you use/call them.
Each function object has its own type.
Ordinary functions have different types only when their signatures differ. However, function objects can have different types even when their signatures are the same. In fact, each functional behavior defined by a function object has its own type. This is a significant improvement for generic programming using templates because you can pass functional behavior as a template parameter. It enables containers of different types to use the same kind of function object as a sorting criterion. This ensures that you don't assign, combine, or compare collections that have different sorting criteria. You can even design hierarchies of function objects so that you can, for example, have different, special kinds of one general criterion.
Function objects are usually faster than ordinary functions.
The concept of templates usually allows better optimization because more details are defined at compile time. Thus, passing function objects instead of ordinary functions often results in better performance.
In the rest of this subsection I present some examples that demonstrate how function objects can be "smarter" than ordinary functions. Chapter 8, which deals only with function objects, provides more examples and details. In particular, it shows how to benefit from the ability to pass functional behavior as a template parameter.
Suppose you want to add a certain value to all elements of a collection. If you know the value you want to add at compile time, you could use an ordinary function:
void add10 (int& elem)
{
elem += 10;
}
void fl()
{
vector<int> coll;
...
for_each (coll.begin(), coll.end(), //range
add10); //operation
}
If you need different values that are known at compile time, you could use a template instead:
template <int theValue>
void add (int& elem)
{
elem += theValue;
}
void f1()
{
vector<int> coll;
...
for_each (coll.begin() , coll.end(), //range
add<10>); //operation
}
If you process the value to add at runtime, things get complicated. You must pass the value to the function before the function is called. This normally results in some global variable that is used both by the function that calls the algorithm and by the function that is called by the algorithm to add that value. This is messy style.
If you need such a function twice, with two different values to add, and both values are processed at runtime, you can't achieve this with one ordinary function. You must either pass a tag or you must write two different functions. Did you ever copy the definition of a function because it had a static variable to keep its state and you needed the same function with another state at the same time? This is exactly the same type of problem.
With function objects, you can write a "smarter" function that behaves in the desired way. Because the object may have a state, it can be initialized by the correct value. Here is a complete example[12]:
// stl/add1.cpp #include <iostream> #include <list> #include <algorithm> #include "print.hpp" using namespace std; //function object that adds the value with which it is initialized class AddValue { private: int the Value; //the value to add public: //constructor initializes the value to add AddValue(int v) : theValue(v) { } //the "function call" for the element adds the value void operator() (int& elem) const { elem += theValue; } }; int main() { list<int> coll;
The first call of for_each() adds 10 to each value:
for_each (coll.begin(), coll.end(), //range AddValue(10)) ; //operation
Here, the expression AddValue(10) creates an object of type AddValue that is initialized with the value 10. The constructor of AddValue stores this value as the member theValue. Inside for_each(), "()" is called for each element of coll. Again, this is a call of operator () for the passed temporary function object of type AddValue. The actual element is passed as an argument. The function object adds its value 10 to each element. The elements then have the following values:
after adding 10: 11 12 13 14 15 16 17 18 19
The second call of for_each() uses the same functionality to add the value of the first element to each element. It initializes a temporary function object of type AddValue with the first element of the collection:
AddValue (*coll. begin())
The output is then as follows:
after adding first element: 22 23 24 25 26 27 28 29 30
See page 335 for a modified version of this example, in which the AddValue function object type is a template for the type of value to add.
By using this technique, two different function objects can solve the problem of having a function with two states at the same time. For example, you could simply declare two function objects and use them independently:
AddValue addx (x); //function object that adds value x AddValue addy (y); //function object that adds value y for_each (coll.begin(),coll.end(), //add value x to each element addx); ... for_each (coll.begin(),coll.end(), //add value y to each element addy); ... for_each (coll.begin() .coll.end(), //add value x to each element addx);
Similarly you can provide additional member functions to query or to change the state of the function object during its lifetime. See page 300 for a good example.
Note that for some algorithms the C++ standard library does not specify how often function objects are called for each element, and it might happen that different copies of the function object are passed to the elements. This might have some nasty consequences if you use function objects as predicates. Section 8.1.4, covers this issue.
The C++ standard library contains several predefined function objects that cover fundamental operations. By using them, you don't have to write your own function objects in several cases. A typical example is a function object used as a sorting criterion. The default sorting criterion for operator < is the predefined sorting criterion less<>. Thus, if you declare
set<int> coll;
it is expanded to[13]
set<int, less<int> > coll; //sort elements with <
From there, it is easy to sort elements in the opposite order[14]:
set<int ,greater<int> > coll; //sort elements with >
Similarly, many function objects are provided to specify numeric processing. For example, the following statement negates all elements of a collection:
transform (coll.begin() , coll.end(), //source coll.begin(), //destination negate<int>()) ; //operation
The expression
negate<int>()
creates a function object of the predefined template class negate that simply returns the negated element of type int for which it is called. The transform() algorithm uses that operation to transform all elements of the first collection into the second collection. If source and destination are equal (as in this case), the returned negated elements overwrite themselves. Thus, the statement negates each element in the collection.
Similarly, you can process the square of all elements in a collection:
//process the square of all elements transform (coll.begin(), coll.end(), //first source coll.begin(), //second source coll.begin(), //destination multiplies<int>()) ; //operation
Here, another form of the transform() algorithm combines elements of two collections by using the specified operation, and writes the resulting elements into the third collection. Again, all collections are the same, so each element gets multiplied by itself, and the result overwrites the old value.[15]
By using special function adapters you can combine predefined function objects with other values or use special cases. Here is a complete example:
// stl/fo1.cpp #include <iostream> #include <set> #include <deque> #include <algorithm> #include "print.hpp" using namespace std; int main() { set<int,greater<int> > coll1; deque<int> coll2; //insert elements from 1 to 9 for (int i=1; i<=9; ++i) { coll1.insert(i); } PRINT.ELEMENTS(coll1,"initialized: "); //transform all elements into coll2 by multiplying 10 transform (coll1 .begin(), coll1 .end(), //source back_inserter(coll2), //destination bind2nd(multiplies<int>() ,10)); //operation PRINT_ELEMENTS(coll2,"transformed: "); //replace value equal to 70 with 42 replace_if (coll2.begin(),coll2.end(), //range bind2nd(equal_to<int>() ,70) , //replace criterion 42) ; //new value PRINT_ELEMENTS(coll2,"replaced: "); //remove all elements with values less than 50 coll2.erase(remove_if(coll2.begin(),coll2.end(), //range bind2nd(less<int>() ,50)), //remove criterion coll2.end()); PRINT_ELEMENTS(coll2,"removed: "); }
With the statement
transform (coll1.begin() ,coll1.end() //source back_inserter (coll2) , //destination bind2nd(multiplies<int>() ,10)) ; //operation
all elements of coll1 are transformed into coll2 (inserting) while multiplying each element by 10. Here, the function adapter bind2nd causes multiply<int> to be called for each element of the source collection as the first argument and the value 10 as the second.
The way bind2nd operates is as follows: transform() is expecting as its fourth argument an operation that takes one argument; namely, the actual element. However, we would like to multiply that argument by ten. So, we have to combine an operation that takes two arguments and the value that always should be used as a second argument to get an operation for one argument. bind2nd does that job. It stores the operation and the second argument as internal values. When the algorithm calls bind2nd with the actual element as the argument, bind2nd calls its operation with the element from the algorithm as the first argument and the internal value as the second argument, and returns the result of the operation.
Similarly, in
replace_if (coll2.begin(),coll2.end(), //range bind2nd(equal_to<int>(),70), //replace criterion 42);
the expression
bind2nd(equal_to<int>(),70)
is used as a criterion to specify the elements that are replaced by 42. bind2nd calls the binary predicate equal_to with value 70 as the second argument, thus defining a unary predicate for the elements of the processed collection.
The last statement is similar because the expression
bind2nd(less<int>(),50)
is used to specify the element that should be removed from the collection. It specifies that all elements that are less than value 50 be removed. The output of the program is as follows:
initialized: 9 8 7 6 5 4 3 2 1 transformed: 90 80 70 60 50 40 30 20 10 replaced: 90 80 42 60 50 40 30 20 10 removed: 90 80 60 50
This kind of programming results in functional composition. What is interesting is that all these function objects are usually declared inline. Thus, you use a function-like notation or abstraction, but you get good performance.
There are other kinds of function objects. For example, some function objects provide the ability to call a member function for each element of a collection:
for_each (coll.begin(), coll.end(), //range mem_fun_ref (&Person: : save)); //operation
The function object mem_fun_ref calls a specified member function for the element for which it is called. Thus, for each element of the collection coll, the member function save() of class Person is called. Of course, this works only if the elements have type Person or a type derived from Person.
Section 8.2, lists and discusses in more detail all predefined function objects, function adapters, and aspects of functional composition. It also explains how you can write your own function objects.
Elements of containers must meet certain requirements because containers handle them in a special way. In this section I describe these requirements. I also discuss the consequences of the fact that containers make copies of their elements internally.
Containers, iterators, and algorithms of the STL are templates. Thus, they can process any type, whether predefined or user defined. However, because of the operations that are called, some requirements apply. The elements of STL containers must meet the following three fundamental requirements:
An element must be copyable by a copy constructor. The generated copy should be equivalent to the source. This means that any test for equality returns that both are equal and that both source and copy behave the same.
All containers create internal copies of their elements and return temporary copies of them, so the copy constructor is called very often. Thus, the copy constructor should perform well (this is not a requirement, but a hint to get better performance). If copying objects takes too much time you can avoid copying objects by using the containers with reference semantics. See Section 6.8, for details.
An element must be assignable by the assignment operator. Containers and algorithms use assignment operators to overwrite old elements with new elements.
An element must be destroyable by a destructor. Containers destroy their internal copies of elements when these elements are removed from the container. Thus, the destructor must not be private. Also, as usual in C++, a destructor must not throw; otherwise, all bets are off.
These three operations are generated implicitly for any class. Thus, a class meets the requirements automatically, provided no special versions of these operations are defined and no special members disable the sanity of those operations.
Elements might also have to meet the following requirements[16]:
For some member functions of sequence containers, the default constructor must be available. For example, it is possible to create a nonempty container or increase the number of elements with no hint of the values those new elements should have. These elements are created without any arguments by calling the default constructor of their type.
For several operations, the test of equality with operator == must be defined. It is especially needed when elements are searched.
For associative containers the operations of the sorting criterion must be provided by the elements. By default, this is the operator <, which is called by the less<> function object.
All containers create internal copies of their elements and return copies of those elements. This means that container elements are equal but not identical to the objects you put into the container. If you modify objects as elements of the container, you modify a copy, not the original object.
Copying values means that the STL containers provide value semantics. They contain the values of the objects you insert rather than the objects themselves. In practice, however, you also need reference semantics. This means that the containers contain references to the objects that are their elements.
The approach of the STL, only to support value semantics, has strengths and weaknesses. Its strengths are:
Copying elements is simple.
References are error prone. You must ensure that references don't refer to objects that no longer exist. You also have to manage circular references, which might occur.
Its weaknesses are:
Copying elements might result in bad performance or may not even be possible.
Managing the same object in several containers at the same time is not possible.
In practice you need both approaches; you need copies that are independent of the original data (value semantics) and copies that still refer to the original data and get modified accordingly (reference semnatics). Unfortunately, there is no support for reference semantics in the C++ standard library. However, you can implement reference semantics in terms of value semantics.
The obvious approach to implementing reference semantics is to use pointers as elements.[17] However, ordinary pointers have the usual problems. For example, objects to which they refer may no longer exist, and comparisons may not work as desired because pointers instead of the objects are compared. Thus, you should be very careful when you use ordinary pointers as container elements.
A better approach is to use a kind of smart pointer — objects that have a pointer-like interface but that do some additional checking or processing internally. The important question here is, how smart do they have to be? The C++ standard library does provide a smart pointer class that might look like it would be useful here: auto_ptr (see Section 4.2). However, you can't use auto_ptrs because they don't meet a fundamental requirement for container elements. That is, after a copy or an assignment of an auto_ptr is made, source and destination are not equivalent. In fact, the source auto_ptr gets modified because its value gets transferred and not copied(see page 43 and page 47). In practice, this means that sorting or even printing the elements of a container might destroy them. So, do not use auto.ptrs as container elements (if you have a standard-conforming C++ system, you will get an error at compile time if you try to use an auto_ptr as a container element). See page 43 for details.
To get reference semantics for STL containers you must write your own smart pointer class. But be aware: Even if you use a smart pointer with reference counting (a smart pointer that destroys its value automatically when the last reference to it gets destroyed), it is troublesome. For example, if you have direct access to the elements, you can modify their values while they are in the container. Thus, you could break the order of elements in an associative container. You don't want to do this.
Section 6.8, offers more details about containers with reference semantics. In particular, it shows a possible way to implement reference semantics for STL containers by using smart pointers with reference counting.
Errors happen. They might be logical errors caused by the program (the programmer) or runtime errors caused by the context or the environment of a program (such as low memory). Both kinds of errors may be handled by exceptions (see page 15 for a short introduction to exceptions). This section discusses how errors and exceptions are handled in the STL.
The design goal of the STL was the best performance rather than the most security. Error checking wastes time, so almost none is done. This is fine if you can program without making any errors, but it can be a catastrophe if you can't. Before the STL was adopted into the C++ standard library, discussions were held regarding whether to introduce more error checking. The majority decided not to, for two reasons:
Error checking reduces performance, and speed is still a general goal of programs. As mentioned, good performance was one of the design goals of the STL.
If you prefer safety over speed, you can still get it, either by adding wrappers or by using special versions of the STL. But you can't program to avoid error checking to get better performance when error checking is built into all basic operations. For example, when every subscript operation checks whether a range is valid, you can't write your own subscripts without checking. However, it is possible the other way around.
As a consequence, error checking is possible but not required inside the STL.
The C++ standard library states that any use of the STL that violates preconditions results in undefined behavior. Thus, if indexes, iterators, or ranges are not valid, the result is undefined. If you do not use a safe version of the STL, undefined memory access typically results, which causes some nasty side effects or even a crash. In this sense, the STL is as error prone as pointers are in C.
Finding such errors could be very hard, especially without a safe version of the STL.
In particular, the use of the STL requires that the following be met:
Iterators must be valid. For example, they must be initialized before they are used. Note that iterators may become invalid as a side effect of other operations. In particular, they become invalid for vectors and deques if elements are inserted or deleted, or reallocation takes place.
Iterators that refer to the past-the-end position have no element to which to refer. Thus, calling operator * or operator -> is not allowed. This is especially true for the return values of the end() and rend() container member functions.
Ranges must be valid:
Both iterators that specify a range must refer to the same container.
The second iterator must be reachable from the first iterator.
If more than one source range is used, the second and later ranges must have at least as many elements as the first one.
Destination ranges must have enough elements that can be overwritten; otherwise, insert iterators must be used.
The following example shows some possible errors:
// stl/iterbug1.cpp #include <iostream> #include <vector> #include <algorithm> using namespace std; int main() { vector<int> coll1; //empty collection vector<int> coll2; //empty collection /* RUNTIME ERROR: * - beginning is behind the end of the range */ vector<int>::iterator pos = coll1.begin(); reverse (++pos, coll1 .end()); //insert elements from 1 to 9 into coll2 for (int i=1; i<=9; ++i) { coll2.push_back (i); } /*RUNTIME ERROR: * - overwriting nonexisting elements */ copy (coll2.begin(), coll2.end(), //source coll1 .begin()) ; //destination /* RUNTIME ERROR: * - collections mistaken * - begin() and end() mistaken */ copy (coll1.begin(), coll2.end(), //source coll1. end()); //destination }
Note that these errors occur at runtime, not at compile time, and thus they cause undefined behavior.
There are many ways to make mistakes when using the STL, and the STL is not required to protect you from yourself. Thus, it is a good idea to use a "safe" STL, at least during software development. A first version of a safe STL was introduced by Cay Horstmann.[18] Unfortunately, most library vendors provide the STL based on the original source code, which doesn't include error handling. But things get better. An exemplary version of the STL is the "STLport," which is available for free for almost any platform at www.stlport.org/.
The STL almost never checks for logical errors. Therefore, almost no exceptions are generated by the STL itself due to a logical problem. In fact, there is only one function call for which the standard requires that it might cause an exception directly: the at() member function for vectors and deques. (It is the checked version of the subscript operator.) Other than that, the standard requires that only the usual standard exceptions may occur, such as bad_alloc for lack of memory or exceptions of user-defined operations.
When are exceptions generated and what happens to STL components when they are? For a long time during the standardization process there was no defined behavior regarding this. In fact, every exception resulted in undefined behavior. Even the destruction of an STL container after an exception was thrown during one of its operations resulted in undefined behavior, such as a crash. Thus, the STL was useless when you needed guaranteed, defined behavior because it was not even possible to unwind the stack.
How to handle exceptions was one of the last topics addressed during the standardization process. Finding a good solution was not easy, and it took a long time for the following reasons:
It was very difficult to determine the degree of safety the C++ standard library should provide. You might argue that it is always best to provide as much safety as possible. For example, you could say that the insertion of a new element at any position in a vector ought to either succeed or have no effect. Ordinarily an exception might occur while copying later elements into the next position to make room for the new element, from which a full recovery is impossible. To achieve the stated goal, the insert operation would need to be implemented to copy every element of the vector into new storage, which would have a serious impact on performance. If good performance is a design goal (as is the case for the STL), you can't provide perfect exception handling in all cases. You have to find a compromise that meets both needs.
There was a concern that the presence of code to handle exceptions could adversely affect performance. This would contradict the design goal of achieving the best possible performance. However, compiler writers state that, in principle, exception handling can be implemented without any significant performance overhead (and many such implementations exist). There is no doubt that it is better to have guaranteed, defined behavior for exceptions without a significant performance penalty instead of the risk that exceptions might crash your system.
As a result of these discussions, the C++ standard library now gives the following basic guarantee for exception safety[19]: The C++ standard library will not leak resources or violate container invariants in the face of exceptions.
Unfortunately, for many purposes this is not enough. Often you need a stronger guarantee that specifies that an operation has no effect if an exception is thrown. Such operations can be considered to be atomic with respect to exceptions. Or, to use terms from database programming, you could say that these operations support commit-or-rollback behavior or are transaction safe.
Regarding this stronger guarantee, the C++ standard library now guarantees the following:
For all node-based containers (lists, sets, multisets, maps and multimaps), any failure to construct a node simply leaves the container as it was. Furthermore, removing a node can't fail (provided destructors don't throw). However, for multiple-element insert operations of associative containers, the need to keep elements sorted makes full recovery from throws impractical. Thus, all single-element insert operations of associative containers support commit-or-rollback behavior. That is, they either succeed or have no effect. In addition, it is guaranteed that all erase operations for both single- and multiple-elements always succeed.
For lists, even multiple-element insert operations are transaction-safe. In fact, all list operations, except remove(), remove_if(), merge(), sort(), and unique(), either succeed or have no effect. For some of them the C++ standard library provides conditional guarantees. Thus, if you need a transaction-safe container, you should use a list.
All array-based containers (vectors and deques) do not fully recover when an element gets inserted. To do this, they would have to copy all subsequent elements before any insert operation, and handling full recovery for all copy operations would take quite a lot of time. However, push and pop operations that operate at the end do not require that existing elements have to get copied. So if they throw, it is guaranteed that they have no effect. Furthermore, if elements have a type with copy operations (copy constructor and assignment operator) that do not throw, then every container operation for these elements either succeeds or has no effect.
See Section 6.10.10, for a detailled overview of all container operations that give stronger guarantees in face of exceptions.
Note that all these guarantees are based on the requirement that destructors never throw (which should always be the case in C++). The C++ standard library makes this promise, and so must the application programmer.
If you need a container that has a full commit-or-rollback ability, you should use either a list (without calling the sort() and unique() member functions) or an associative container (without calling their multiple-element insert operations). This avoids having to make copies before a modifying operation to ensure that no data gets lost. Note that making copies of a container could be very expensive.
If you can't use a node-based container and need the full commit-or-rollback ability, you have to provide wrappers for each critical operation. For example, the following function would almost safely insert a value in any container at a certain position:
template <class T, class Cont, class Iter>
void insert (const Cont& coll, Iter pos, const T& value)
{
Cont tmp(coll); //copy container and all elements
tmp. insert (pos, value); //modify the copy
coll. swap (tmp); //use copy (in case no exception was thrown)
}
Note that I wrote "almost," because this function still is not perfect. This is because the swap() operation throws when, for associative containers, copying the comparison criterion throws. You see, handling exceptions perfectly is not easy.
The STL is designed as a framework that may be extended in almost any direction. You can supply your own containers, iterators, algorithms, or function objects, provided they meet certain requirements. In fact, there are some useful extensions that are missing in the C++ standard library. This happened because at some point the committee had to stop introducing new features and concentrate on perfecting the existing parts; otherwise, the job would never have been completed.
The most important component that is missing in the STL is an additional kind of container that is implemented as a hash table. The proposal of having hash tables be part of the C++ standard library simply came too late. However, newer versions of the standard will likely contain some form of hash tables. Most implementations of the C++ library already provide hash containers, but unfortunately they're all different. See Section 6.7.3, for more details.
Other useful extensions are some additional function objects (see Section 8.3), iterators (see Section 7.5.2), containers (see Section 6.7), and algorithms (see Section 7.5.1).
[1] The National Institute of Health's Class Library was one of the first class libraries in C++.
[2] Strictly speaking, appending elements is amortized very fast. An individual append may be slow, when a vector has to reallocate new memory and to copy existing elements into the new memory. However, because such reallocations are rather rare, the operation is very fast in the long term. See page 22 for a discussion of complexity.
[3] It is only a mere accident that "deque" also sounds like "hack" :-).
[4] For other character sets the output may contain characters that aren't letters or it may even be empty (if 'z' is not greater than 'a').
[5] In some older environments, operator -> might not work yet for iterators.
[6] Note that you have to put a space between the two ">" characters. ">>" would be parsed as shift operator, which would result in a syntax error.
[7] In some older environments, operator -> might not work yet for iterators. In this case, you must use the second version.
[8] A stream is an object that represents I/O channels (see Chapter 13).
[9] In older systems you must use ptrdiff_t as the second template parameter to create an istream iterator (see Section 7.4.3).
[10] The definition of distance() has changed, so in older STL versions you must include the file distance.hpp, which is mentioned on page 263.
[11] Unfortunately, some systems provide really bad error handling. You see that something went wrong but have problems finding out why. Some compilers don't even print the source code that caused the trouble. This will change in the future, I hope.
[12] The auxiliary function PRINT_ELEMENTS() was introduced on page 118.
[13] For systems that don't provide default template arguments, you usually must use the latter form.
[14] Note that you have to put a space between the two ">" characters. ">>" would be parsed as shift operator, which would result in a syntax error.
[15] In earlier versions of the STL, the function object for multiplication had the name times. This was changed due to a name clash with a function of operating system standards (X/Open, POSIX) and because multiplies was clearer.
[16] In some older C++ systems, you may have to implement these additional requirements even if they are not used. For example, some implementations of vector always require the default constructor for elements. Other implementations always require the existence of the comparison operator. However, according to the standard, such a requirement is wrong, and these limitations will likely be eliminated.
[17] C programmers might recognize the use of pointers to get reference semantics. In C, function arguments are able to get passed only by value, so you need pointers to enable a call-by-reference.
[18] You can find the safe STL by Cay Horstmann at www.horstmann.com/safestl.html.
[19] Many thanks to Dave Abrahams and Greg Colvin for their work on exception safety in the C++ standard library and for the feedback they gave me regarding this topic.
| CONTENTS |
| Browser Based Help. Published by chm2web software. |