| CONTENTS |
This chapter discusses STL containers in detail. It continues the discussion that was begun in Chapter 5. The chapter starts with a general overview of the general abilities and operations of all container classes, with each container class explained in detail. The explanation includes a description of their internal data structures, their operations, and their performance. It also shows how to use the different operations and gives examples if the usage is not trivial. Each section about the containers ends with examples of the typical use of the container. The chapter then discusses the interesting question of when to use which container. By comparing the general abilities, advantages, and disadvantages of all container types, it shows you how to find the best container to meet your needs. Lastly, the chapter covers all members of all container classes in detail. This part is intended as a type of reference manual. You can find the minor details of the container interface and the exact signature of the container operations. When useful, crossreferences to similar or supplementary algorithms are included.
The C++ standard library provides some special container classes, the so-called container adapters (stack, queue, priority queue), bitmaps, and valarrays. All of these have special interfaces that don't meet the general requirements of STL containers, so they are covered in separate sections.[1] Container adapters and bitsets are covered in Chapter 10. Valarrays are described in Section 12.2
This section covers the common abilities of STL container classes. Most of them are requirements that, in general, every STL container should meet. The three core abilities are as follows:
All containers provide value rather than reference semantics. Containers copy elements internally when they are inserted rather than managing references to it. Thus, each element of an STL container must be able to be copied. If objects you want to store don't have a public copy constructor, or copying is not useful (for example, because it takes time or elements must be part of multiple containers), the container elements must be pointers or pointer objects that refer to these objects. Section 5.10.2, covers this problem in detail.
In general, all elements have an order. Thus, you can iterate one or many times over all elements in the same order. Each container type provides operations that return iterators to iterate over the elements. This is the key interface of the STL algorithms.
In general, operations are not safe. The caller must ensure that the parameters of the operations meet the requirements. Violating these requirements (such as using an invalid index) results in undefined behavior. Usually the STL does not throw exceptions by itself. If user-defined operations called by the STL containers do throw, the behavior is different. See Section 5.11.2, for details.
The operations common to all containers meet the core abilities that were mentioned in the previous subsection. Table 6.1 lists these operations. The following subsections explore some of these common operations.
Every container class provides a default constructor, a copy constructor, and a destructor. You can also initialize a container with elements of a given range. This constructor is provided to initialize the container with elements of another container, with an array, or from standard input. These constructors are member templates (see page 11), so not only the container but also the type of the elements may differ, provided there is an automatic conversion from the source element type to the destination element type.[2] The following examples expand on this:
| Operation | Effect |
|---|---|
| ContType c | Creates an empty container without any element |
| ContType c1(c2) | Copies a container of the same type |
| ContType c(beg,end) | Creates a container and initializes it with copies of all elements of [beg,end) |
| c.~ContType() | Deletes all elements and frees the memory |
| c.size() | Returns the actual number of elements |
| c.empty() | Returns whether the container is empty (equivalent to size()==0, but might be faster) |
| c.max_size() | Returns the maximum number of elements possible |
| c1 == 2 | Returns whether c1 is equal to c2 |
| c1 != c2 | Returns whether c1 is not equal to c2 (equivalent to !(c1==c2)) |
| c1 < c2 | Returns whether c1 is less than c2 |
| c1 > c2 | Returns whether c1 is greater than c2 (equivalent to c2<c1 |
| c1 <= c2 | Returns whether c1 is less than or equal to c2 (equivalent to !(c2<c1)) |
| c1 >= c2 | Returns whether c1is greater than or equal to c2 (equivalent to !(c1<c2)) |
| c1 = c2 | Assigns all elements of c1 to c2 |
| c1.swap(c2) | Swaps the data of c1and c2 |
| swap(c1,c2) | Same (as global function) |
| c.begin() | Returns an iterator for the first element |
| c.end() | Returns an iterator for the position after the last element |
| c.rbegin() | Returns a reverse iterator for the first element of a reverse iteration |
| c.rend() | Returns a reverse iterator for the position after the last element of a reverse iteration |
| c.insert(pos,elem) | Inserts a copy of elem (return value and the meaning of pos differ) |
| c.erase(beg,end) | Removes all elements of the range [beg,end) (some containers return next element not removed) |
| c.clar() | Removes all elements (makes the container empty) |
| c.get_allocator() | Returns the memory model of the container |
Initialize with the elements of another container:
std::list<int> l; //l is a linked list of ints ... //copy all elements of the list as floats into a vector std::vector<float> c(l.begin(),l.end());
Initialize with the elements of an array:
int array[] = { 2, 3, 17, 33, 45, 77 };
...
//copy all elements of the array into a set
std::set<int> c(array,array+sizeof(array)/sizeof(array[0]));
Initialize by using standard input:
//read all integer elements of the deque from standard input
std::deque<int> c((std::istream_iterator<int>(std::cin)),
(std::istream_iterator<int>()));
Don't forget the extra parentheses around the initializer arguments here. Otherwise, this expression does something very different and you probably will get some strange warnings or errors in following statements. Consider writing the statement without extra parentheses:
std::deque<int> c(std::istream_iterator<int>(std::cin),
std::istream_iterator<int>());
In this case, c declares a function with a return type that is deque<int>. Its first parameter is of type istream_iterator<int> with the name cin, and its second unnamed parameter is of type "function taking no arguments returning istream_iterator<int>." This construct is valid syntactically as either a declaration or an expression. So, according to language rules, it is treated as a declaration. The extra parentheses force the initializer not to match the syntax of a declaration.[3]
In principle, these techniques are also provided to assign or to insert elements from another range. However, for those operations the exact interfaces either differ due to additional arguments or are not provided for all container classes.
For all container classes, three size operations are provided:
size()
Returns the actual number of elements of the container.
empty()
Is a shortcut for checking whether the number of elements is zero (size()==0). However, empty() might be implemented more efficiently, so you should use it if possible.
max_size()
Returns the maximum number of elements a container might contain. This value is implementation defined. For example, a vector typically contains all elements in a single block of memory, so there might be relevant restrictions on PCs. Otherwise, max_size() is usually the maximum value of the type of the index.
The usual comparison operators ==, ! =, <, <=, >, and >= are defined according to the following three rules:
Both containers must have the same type.
Two containers are equal if their elements are equal and have the same order. To check equality of elements, use operator ==.
To check whether a container is less than another container, a lexicographical comparison is done(see page 360).
To compare containers with different types, you must use the comparing algorithms of Section 9.5.4.
If you assign containers, you copy all elements of the source container and remove all old elements in the destination container. Thus, assignment of containers is relatively expensive.
If the containers have the same type and the source is no longer used, there is an easy optimization: Use swap(). swap() offers much better efficiency because it swaps only the internal data of the containers. In fact, it swaps only some internal pointers that refer to the data (elements, allocator, sorting criterion, if any). So, swap() is guaranteed to have only constant complexity, instead of the linear complexity of an assignment.
A vector models a dynamic array. Thus, it is an abstraction that manages its elements with a dynamic array (Figure 6.1). However, note that the standard does not specify that the implementation use a dynamic array. Rather, it follows from the constraints and specification of the complexity of its operation.

To use a vector, you must include the header file <vector>[4]:
#include <vector>
There, the type is defined as a template class inside namespace std:
namespace std {
template <class T,
class Allocator = allocator<T> >
class vector;
}
The elements of a vector may have any type T that is assignable and copyable. The optional second template parameter defines the memory model (see Chapter 15). The default memory model is the model allocator, which is provided by the C++ standard library.[5]
Vectors copy their elements into their internal dynamic array. The elements always have a certain order. Thus, vectors are a kind of ordered collection. Vectors provide random access. Thus, you can access every element directly in constant time, provided you know its position. The iterators are random access iterators, so you can use any algorithm of the STL.
Vectors provide good performance if you append or delete elements at the end. If you insert or delete in the middle or at the beginning, performance gets worse. This is because every element behind has to be moved to another position. In fact, the assignment operator would be called for every following element.
Part of the way in which vectors give good performance is by allocating more memory than they need to contain all their elements. To use vectors effectively and correctly you should understand how size and capacity cooperate in a vector.
Vectors provide the usual size operations size(), empty(), and max_size() (see Section 6.1.2). An additional "size" operation is the capacity() function. capacity() returns the number of characters a vector could contain in its actual memory. If you exceed the capacity(), the vector has to reallocate its internal memory.
The capacity of a vector is important for two reasons:
Reallocation invalidates all references, pointers, and iterators for elements of the vector.
Reallocation takes time.
Thus, if a program manages pointers, references, or iterators into a vector, or if speed is a goal, it is important to take the capacity into account.
To avoid reallocation, you can use reserve() to ensure a certain capacity before you really need it. In this way, you can ensure that references remain valid as long as the capacity is not exceeded:
std::vector<int> v; // create an empty vector v.reserve (80); // reserve memory for 80 elements
Another way to avoid reallocation is to initialize a vector with enough elements by passing additional arguments to the constructor. For example, if you pass a numeric value as parameter, it is taken as the starting size of the vector:
std::vector<T> v(5); // creates a vector and initializes it with five values // (calls five times the default constructor of type T)
Of course, the type of the elements must provide a default constructor for this ability. But note that for complex types, even if a default constructor is provided, the initialization takes time. If the only reason for initialization is to reserve memory, you should use reserve().
The concept of capacity for vectors is similar to that for strings (see Section 11.2.5), with one big difference: Unlike strings, it is not possible to call reserve() for vectors to shrink the capacity. Calling reserve() with an argument that is less than the current capacity is a no-op. Furthermore, how to reach an optimal performance regarding speed and memory usage is implementation defined. Thus, implementations might increase capacity in larger steps. In fact, to avoid internal fragmentation, many implementations allocate a whole block of memory (such as 2K) the first time you insert anything if you don't call reserve() first yourself. This can waste Jots of memory if you have many vectors with only a few small elements.
Because the capacity of vectors never shrinks, it is guaranteed that references, pointers, and iterators remain valid even when elements are deleted or changed, provided they refer to a position before the manipulated elements. However, insertions may invalidate references, pointers, and iterators.
There is a way to shrink the capacity indirectly: Swapping the contents with another vector swaps the capacity. The following function shrinks the capacity while preserving the elements:
template <class T>
void shrinkCapacity(std::vector<T>& v)
{
std::vector<T> tmp(v); // copy elements into a new vector
v.swap(tmp); // swap internal vector data
}
You can even shrink the capacity without calling this function by calling the following statement[6]:
//shrink capacity of vector v for type T std::vector<T>(v).swap(v);
However, note that after swap(), all references, pointers, and iterators swap their containers. They still refer to the elements to which they referred on entry. Thus, shrinkCapacity() invalidates all references, pointers, and iterators.
Table 6.2 lists the constructors and destructors for vectors. You can create vectors with and without elements for initialization. If you pass only the size, the elements are created with their default constructor. Note that an explicit call of the default constructor also initializes fundamental types such as int with zero (this language feature is covered on page 14). See Section 6.1.2, for some remarks about possible initialization sources.
| Operation | Effect |
|---|---|
| vector<Elem> c | Creates an empty vector without any elements |
| vector<Elem> c1(c2) | Creates a copy of another vector of the same type (all elements are copied) |
| vector<Elem> c(n) | Creates a vector with n elements that are created by the default constructor |
| vector<Elem> c(n,elem) | Creates a vector initialized with n copies of element elem |
| vector<Elem> c(beg,end) | Creates a vector initialized with the elements of the range [beg,end) |
| c.~vector<Elem>() | Destroys all elements and frees the memory |
Table 6.3 lists all nonmodifying operations of vectors.[7] See additional remarks in Section 6.1.2, and Section 6.2.1.
| Operation | Effect |
|---|---|
| c.size() | Returns the actual number of elements |
| c.empty() | Returns whether the container is empty (equivalent to size()==0, but might be faster) |
| c.max_size() | Returns the maximum number of elements possible |
| capacity() | Returns the maximum possible number of elements without reallocation |
| reserve() | Enlarges capacity, if not enough yet |
| c1 == c2 | Returns whether c1 is equal to c2 |
| c1 != c2 | Returns whether c1 is not equal to c2 (equivalent to ! (c1==c2)) |
| c1 < c2 | Returns whether c1 is less than c2 |
| c1 > c2 | Returns whether c1 is greater than c2 (equivalent to c2<c1) |
| c1 <= c2 | Returns whether c1 is less than or equal to c2 (equivalent to ! (c2<c1)) |
| c1 >= c2 | Returns whether c1 is greater than or equal to c2 (equivalent to ! (c1<c2)) |
| Operation | Effect |
|---|---|
| c1 = c2 | Assigns all elements of c2 to c1 |
| c.assign(n,elem) | Assigns n copies of element elem |
| c.assign(beg,end) | Assigns the elements of the range [beg,end) |
| c1.swap(c2) | Swaps the data of c1 and c2 |
| swap(c1,c2) | Same (as global function) |
Table 6.4 lists the ways to assign new elements while removing all ordinary elements. The set of assign() functions matches the set of constructors. You can use different sources for assignments (containers, arrays, standard input) similar to those described for constructors on page 144. All assignment operations call the default constructor, copy constructor, assignment operator, and/or destructor of the element type, depending on how the number of elements changes. For example:
std::list<Elem> l;
std::vector<Elem> coll;
...
//make coll be a copy of the contents of l
coll.assign(l.begin(),l.end());
Table 6.5 shows all vector operations for direct element access. As usual in C and C++, the first element has index 0 and the last element has index size()-1. Thus, the nth element has index n-1. For nonconstant vectors, these operations return a reference to the element. Thus you could modify an element by using one of these operations (provided it is not forbidden for other reasons).
| Operation | Effect |
|---|---|
| c.at(idx) | Returns the element with index idx (throws range error exception if idx is out of range) |
| c[idx] | Returns the element with index idx (no range checking) |
| c.front() | Returns the first element (no check whether a first element exists) |
| c.back() | Returns the last element (no check whether a last element exists) |
The most important issue for the caller is whether these operations perform range checking. Only at() performs range checking. If the index is out of range, it throws an out_of_range exception (see Section 3.3). All other functions do not check. A range error results in undefined behavior. Calling operator [], front(), and back() for an empty container always results in undefined behavior:
std::vector<Elem> coll; // empty! coll [5] = elem; // RUNTIME ERRORundefined behavior std::cout << coll. front (); // RUNTIME ERROR
undefined behavior
So, you must ensure that the index for operator [] is valid and the container is not empty when either front() or back() is called:
std::vector<Elem> coll; // empty! if (coll.size() > 5) { coll [5] = elem; // OK } if (!coll.empty()) { cout << coll.front(); // OK } coll.at(5) = elem; // throws out_of_range exception
Vectors provide the usual operators to get iterators (Table 6.6). Vector iterators are random access iterators (see Section 7.2, for a discussion of iterator categories). Thus, in principle you could use all algorithms of the STL.
| Operation | Effect |
|---|---|
| c.begin() | Returns a random access iterator for the first element |
| c.end() | Returns a random access iterator for the position after the last element |
| c.rbegin() | Returns a reverse iterator for the first element of a reverse iteration |
| c.rend() | Returns a reverse iterator for the position after the last element of a reverse iteration |
The exact type of these iterators is implementation defined. However, for vectors they are often ordinary pointers. An ordinary pointer is a random access iterator, and because the internal structure of a vector is usually an array, it has the correct behavior. However, you can't count on it. For example, if a safe version of the STL that checks range errors and other potential problems is used, the iterator type is usually an auxiliary class. See Section 7.2.6, for a look at the nasty difference between iterators implemented as pointers and iterators implemented as classes.
Iterators remain valid until an element with a smaller index gets inserted or removed, or reallocation occurs and capacity changes (see Section 6.2.1).
Table 6.7 shows the operations provided for vectors to insert or to remove elements. As usual by using the STL, you must ensure that the arguments are valid. Iterators must refer to valid positions, the beginning of a range must have a position that is not behind the end, and you must not try to remove an element from an empty container.
Regarding performance, you should consider that inserting and removing happens faster when
Elements are inserted or removed at the end
The capacity is large enough on entry
Multiple elements are inserted by a single call rather than by multiple calls
Inserting or removing elements invalidates references, pointers, and iterators that refer to the following elements. If an insertion causes reallocation, it invalidates all references, iterators, and pointers.
| Operation | Effect |
|---|---|
| c.insert(pos,elem) | Inserts at iterator position pos a copy of elem and returns the position of the new element |
| c.insert(pos,n,elem) | Inserts at iterator position pos n copies of elem (returns nothing) |
| c.insert(pos,beg,end) | Inserts at iterator position pos a copy of all elements of the range [beg,end) (returns nothing) |
| c.push_back(elem) | Appends a copy of elem at the end |
| c.pop_back() | Removes the last element (does not return it) |
| c.erase(pos) | Removes the element at iterator position pos and returns the position of the next element |
| c.erase(beg,end) | Removes all elements of the range [beg,end) and returns the position of the next element |
| c.resize(num) | Changes the number of elements to num (if size() grows, new elements are created by their default constructor) |
| c.resize(num,elem) | Changes the number of elements to num (if size() grows, new elements are copies of elem) |
| c.clear() | Removes all elements (makes the container empty) |
Vectors provide no operation to remove elements directly that have a certain value. You must use an algorithm to do this. For example, the following statement removes all elements that have the value val:
std::vector<Elem> coll;
...
//remove all elements with value val
coll.erase(remove(coll.begin(),coll.end(),
val),
coll.end());
This statement is explained in Section 5.6.1.
To remove only the first element that has a certain value, you must use the following statements:
std::vector<Elem> coll;
...
//remove first element with value val
std::vector<Elem>::iterator pos;
pos = find(coll.begin(),coll.end(),
val);
if (pos != coll.end()) {
coll.erase(pos);
}
The C++ standard library does not state clearly whether the elements of a vector are required to be in contiguous memory. However, it is the intention that this is guaranteed and it will be fixed due to a defect report. Thus, you can expect that for any valid index i in vector v, the following yields true:
&v[i] == &v[0] + i
This guarantee has some important consequences. It simply means that you can use a vector in all cases in which you could use a dynamic array. For example, you can use a vector to hold data of ordinary C-strings of type char* or const char*:
std::vector<char> v; // create vector as dynamic array of chars v.resize(41); // make room for 41 characters (including '\0') strcpy(&v[0], "hello, world"); // copy a C-string into the vector printf("%s\n", &v[0]); // print contents of the vector as C-string
Of course, you have to be careful when you use a vector in this way (like you always have to be careful when using dynamic arrays). For example, you have to ensure that the size of the vector is big enough to copy some data into it and that you have an '\0' element at the end if you use the contents as a C-string. However, this example shows that whenever you need an array of type T for any reason (such as for an existing C library) you can use a vector<T> and pass the address of the first element.
Note that you must not pass an iterator as the address of the first element. Iterators of vectors have an implementation-specific type, which may be totally different from an ordinary pointer:
printf("%s\n", v.begin()); // ERROR (might work, but not portable)
printf("%s\n", &v[0]); // OK
Vectors provide only minimal support for logical error checking. The only member function for which the standard requires that it may throw an exception is at(), which is the safe version of the subscript operator (see page 152). In addition, the standard requires that only the usual standard exceptions may occur, such as bad_alloc for a lack of memory or exceptions of user-defined operations.
If functions called by a vector (functions for the element type or functions that are user supplied) throw exceptions, the C++ standard library guarantees the following:
If an element gets inserted with push_back() and an exception occurs, this function has no effect.
insert() either succeeds or has no effect if the copy operations (copy constructor and assignment operator) of the elements do not throw.
pop_back() does not throw any exceptions.
erase() and clear do not throw if the copy operations (copy constructor and assignment operator) of the elements do not throw.
swap() does not throw.
If elements are used that never throw exceptions on copy operations (copy constructor and assignment operator), every operation is either successful or has no effect. Such elements might be "plain old data" (POD). POD describes types that use no special C++ feature. For example, every ordinary C structure is POD.
All these guarantees are based on the requirements that destructors don't throw. See Section 5.11.2, for a general discussion of exceptions handling in the STL and Section 6.10.10, for a list of all container operations that give special guarantees in face of exceptions.
The following example shows a simple usage of vectors:
// cont/vector1.cpp #include <iostream> #include <vector> #include <string> #include <algorithm> using namespace std; int main() { //create empty vector for strings vector<string> sentence; //reserve memory for five elements to avoid reallocation sentence.reserve(5); //append some elements sentence.push_back("Hello,"); sentence.push_back("how"); sentence.push_back("are"); sentence.push_back("you"); sentence.push_back("?"); //print elements separated with spaces copy (sentence.begin(), sentence.end(), ostream_iterator<string>(cout," ")); cout << endl; //print ''technical data'' cout << " max_size(): " << sentence.max_size() << endl; cout << " size(): " << sentence.size() << endl; cout << " capacity(): " << sentence.capacity() << endl; //swap second and fourth element swap (sentence[1], sentence [3]); //insert element "always" before element "?" sentence.insert (find(sentence.begin(),sentence.end(),"?"), "always"); //assign "!" to the last element sentence.back() = "!"; //print elements separated with spaces copy (sentence.begin(), sentence.end(), ostream_iterator<string>(cout," ")); cout << endl; //print "technical data" again cout << " max_size(): " << sentence.max_size() << endl; cout << " size(): " << sentence.size() << endl; cout << " capacity(): " << sentence.capacity() << endl; }
The output of the program might look like this:
Hello, how are you ?
max_size(): 268435455
size(): 5
capacity(): 5
Hello, you are how always !
max_size(): 268435455
size(): 6
capacity(): 10
Note my use of the word "might." The values of max_size() and capacity() are implementation defined. Here, for example, you can see that the implementation doubles the capacity if the capacity no longer fits.
For Boolean elements of a vector, the C++ standard library provides a specialization of vector. The goal is to have a version that is optimized to use less size than a usual implementation of vector for type bool. Such a usual implementation would reserve at least 1 byte for each element. The vector<bool> specialization usually uses internally only 1 bit for an element, so it is typically eight times smaller. Note that such an optimization also has a snag: In C++, the smallest addressable value must have a size of at least 1 byte. Thus, such a specialization of a vector needs special handling for references and iterators.
As a result, a vector<bool> does not meet all requirements of other vectors (for example, a vector<bool>::reference is not a true lvalue and vector<bool>::iterator is not a random access iterator). Therefore, template code might work for vectors of any type except bool. In addition, vector<bool> might perform slower than normal implementations because element operations have to be transformed into bit operations. However, how vector<bool> is implemented is implementation specific. Thus, the performance (speed and memory) might differ.
Note that class vector<bool> is more than a specialization of vector<> for bool. It also provides some special bit operations. You can handle bits or flags in a more convenient way.
vector<bool> has a dynamic size, so you can consider it a bitfield with dynamic size. Thus, you can add and remove bits. If you need a bitfield with static size, you should use bitset rather than a vector<bool>. Class bitset is covered in Section 10.4.
| Operation | Effect |
|---|---|
| c.flip() | Negates all Boolean elements (complement of all bits) |
| m[idx].flip() | Negates the Boolean element with index idx (complement of a single bit) |
| m[idx] = val | Assigns val to the Boolean element with index idx (assignment to a single bit) |
| m[idx1] = m[idx2] | Assigns the value of the element with index idx2 to the element with index idx1 |
The additional operations of vector<bool> are shown in Table 6.8. The operation flip(), which processes the complement, can be called for all bits and a single bit of the vector. Note that you can call flip() for a single Boolean element. This is surprising, because you might expect that the subscript operator returns bool and that calling flip() for such a fundamental type is not possible. Here the class vector<bool> uses a common trick, called a proxy[8]: For vector<bool>, the return type of the subscript operator (and other operators that return an element) is an auxiliary class. If you need the return value to be bool, an automatic type conversion is used. For other operations, the member functions are provided. The relevant part of the declaration of vector<bool> looks like this:
namespace std {
class vector<bool> {
public:
//auxiliary type for subscript operator
class reference {
...
public:
//automatic type conversion to bool
operator bool() const;
//assignments
reference& operator= (const bool);
reference& operator= (const reference&);
//bit complement
void flip();
}
...
//operations for element access
//-return type is reference instead of bool
reference operator[](size_type n);
reference at(size_type n);
reference front();
reference back();
...
};
}
As you can see, all member functions for element access return type reference. Thus, you could also use the following statement:
c.front().flip(); // negate first Boolean element c.at(5) = c.back(); // assign last element to element with index 5
As usual, to avoid undefined behavior, the caller must ensure that the first, last, and sixth elements exist.
The internal type reference is only used for nonconstant containers of type vector<bool>. The constant member functions for element access return ordinary values of type bool.
A deque (pronounced "deck") is very similar to a vector. It manages its elements with a dynamic array, provides random access, and has almost the same interface as a vector. The difference is that with a deque the dynamic array is open at both ends. Thus, a deque is fast for insertions and deletions at both the end and the beginning (Figure 6.2).

To provide this ability, the deque is implemented typically as a bunch of individual blocks, with the first block growing in one direction and the last block growing in the opposite direction (Figure 6.3).
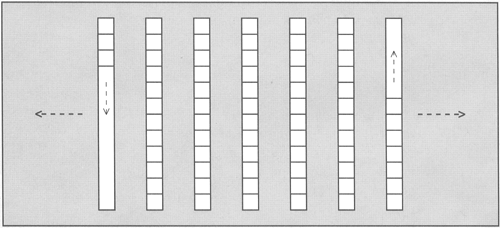
To use a deque, you must include the header file <deque>[9]:
#include <deque>
There, the type is defined as a template class inside namespace std:
namespace std {
template <class T,
class Allocator = allocator<T> >
class deque;
}
As with vectors, the type of the elements is passed as a first template parameter and may be of any type that is assignable and copyable. The optional second template argument is the memory model, with allocator as the default (see Chapter 15).[10]
Deques have the following differences compared with the abilities of vectors:
Inserting and removing elements is fast both at the beginning and at the end (for vectors it is only fast at the end). These operations are done in amortized constant time.
The internal structure has one more indirection to access the elements, so element access and iterator movement of deques are usually a bit slower.
Iterators must be smart pointers of a special type rather than ordinary pointers because they must jump between different blocks.
In systems that have size limitations for blocks of memory (for example, some PC systems), a deque might contain more elements because it uses more than one block of memory. Thus, max_size() might be larger for deques.
Deques provide no support to control the capacity and the moment of reallocation. In particular, any insertion or deletion of elements other than at the beginning or end invalidates all pointers, references, and iterators that refer to elements of the deque. However, reallocation may perform better than for vectors, because according to their typical internal structure, deques don't have to copy all elements on reallocation.
Blocks of memory might get freed when they are no longer used, so the memory size of a deque might shrink (however, whether and how this happens is implementation specific).
The following features of vectors also apply to deques:
Inserting and deleting elements in the middle is relatively slow because all elements up to either of both ends may be moved to make room or to fill a gap.
Iterators are random access iterators.
In summary, you should prefer a deque if the following is true:
You insert and remove elements at both ends (this is the classic case for a queue).
You don't refer to elements of the container.
It is important that the container frees memory when it is no longer used (however, the standard does not guarantee that this happens).
The interface of vectors and deques is almost the same, so trying both is very easy when no special feature of a vector or a deque is necessary.
Table 6.9 through Table 6.11 list all operations provided for deques.
| Operation | Effect |
| deque<Elem> c | Creates an empty deque without any elements |
| deque<Elem> c1(c2) | Creates a copy of another deque of the same type (all elements are copied) |
| deque<Elem> c(n) | Creates a deque with n elements that are created by the default constructor |
| deque<Elem> c(n,elem) | Creates a deque initialized with n copies of element elem |
| deque<Elem> c(beg,end) | Creates a deque initialized with the elements of the range [beg,end) |
| c.~deque<Elem>() | Destroys all elements and frees the memory |
| Operation | Effect |
| c.size() | Returns the actual number of elements |
| c.empty () | Returns whether the container is empty (equivalent to size()==0, but might be faster) |
| c.max_size() | Returns the maximum number of elements possible |
| c1 == c2 | Returns whether c1 is equal to c2 |
| c1 != c2 | Returns whether c1 is not equal to c2 (equivalent to ! (c1==c2)) |
| c1 < c2 | Returns whether c1 is less than c2 |
| c1 > c2 | Returns whether c1 is greater than c2 (equivalent to c2<c1) |
| c1 <= c2 | Returns whether c1 is less than or equal to c2 (equivalent to ! (c2<c1) ) |
| c1 >= c2 | Returns whether c1 is greater than or equal to c2 (equivalent to ! (c1<c2) ) |
| c.at(idx) | Returns the element with index idx (throws range error exception if idx is out of range) |
| c[idx] | Returns the element with index idx (no range checking) |
| c.front() | Returns the first element (no check whether a first element exists) |
| c.back() | Returns the last element (no check whether a last element exists) |
| c.begin() | Returns a random access iterator for the first element |
| c.end() | Returns a random access iterator for the position after the last element |
| c.rbegin() | Returns a reverse iterator for the first element of a reverse iteration |
| c.rend() | Returns a reverse iterator for the position after the last element of a reverse iteration |
| Operation | Effect |
| c1 = c2 | Assigns all elements of c2 to c1 |
| c.assign (n,elem) | Assigns n copies of element elem |
| c.assign (beg,end) | Assigns the elements of the range [beg,end) |
| c1.swap(c2) | Swaps the data of c1 and c2 |
| swap(c1,c2) | Same (as global function) |
| c.insert (pos,elem) | Inserts at iterator position pos a copy of elem and returns the position of the new element |
| c. insert (pos,n,elem) | Inserts at iterator position pos n copies of elem (returns nothing) |
| c.insert (pos,beg,end) | Inserts at iterator position pos a copy of all elements of the range [beg,end) (returns nothing) |
| c.push_back (elem) | Appends a copy of elem at the end |
| c.pop_back() | Removes the last element (does not return it) |
| c.push_front (elem) | Inserts a copy of elem at the beginning |
| c.pop_front() | Removes the first element (does not return it) |
| c.erase(pos) | Removes the element at iterator position pos and returns the position of the next element |
| c.erase (beg,end) | Removes all elements of the range [beg,end) and returns the position of the next element |
| c. resize (num) | Changes the number of elements to num (if size () grows, new elements are created by their default constructor) |
| c.resize (num, elem) | Changes the number of elements to num (if size () grows, new elements are copies of elem) |
| c.clear() | Removes all elements (makes the container empty) |
Deque operations differ from vector operations only as follows:
Deques do not provide the functions for capacity (capacity () and reserve ()).
Deques do provide direct functions to insert and to delete the first element (push_front () and pop_front()).
Because the other operations are the same, they are not reexplained here. See Section 6.2.2, for a description of them.
Note that you still must consider the following:
No member functions for element access (except at ()) check whether an index or an iterator isvalid.
An insertion or deletion of elements might cause a reallocation. Thus, any insertion or deletioninvalidates all pointers, references, and iterators that refer to other elements of the deque. Theexception is when elements are inserted at the front or the back. In this case, references andpointers to elements stay valid (but iterators don't).
In principle, deques provide the same support for exception handing as do vectors (see page 155). The additional operations push_front() and pop_front() behave according to push_back() and pop_back () respectively. Thus, the C++ standard library provides the following behavior:
If an element gets inserted with push_back () or push_front () and an exception occurs, these functions have no effect.
Neither pop_back () nor pop_front () throw any exceptions.
See Section 5.11.2, for a general discussion of exceptions handling in the STL and Section 6.10.10, for a list of all container operations that give special guarantees in face of exceptions.
The following program is a simple example that shows the abilities of deques:
// cont/deque1. cpp #include <iostream> #include <deque> #include <string> #include <algorithm> using namespace std; int main() { //create empty deque of strings deque<string> coll; //insert several elements coll.assign (3, string("string")); coll.push_back ("last string"); coll.push_front ("first string"); //print elements separated by newlines copy (coll.begin(), coll.end(), ostream_iterator<string>(cout,"\n")); cout << endl; //remove first and last element coll.pop_front(); coll.pop_back(); //insert ''another'' into every element but the first for (int i=1; i<coll.size(); ++i) { coll[i] = "another " + coll [i]; } //change size to four elements coll.resize (4, "resized string"); //print elements separated by newlines copy (coll.begin(), coll.end(), ostream_iterator<string>(cout,"\n")); }
The program has the following output:
first string string string string last string string another string another string resized string
A list manages its elements as a doubly linked list (Figure 6.4). As usual, the C++ standard library does not specify the kind of the implementation, but it follows from the list's name, constraints, and specifications.

To use a list you must include the header file <list>[11]:
#include <list>
There, the type is defined as a template class inside namespace std:
namespace std {
template <class T,
class Allocator = allocator<T> >
class list;
}
The elements of a list may have any type T that is assignable and copyable. The optional second template parameter defines the memory model (see Chapter 15). The default memory model is the model allocator, which is provided by the C++ standard library.[12]
The internal structure of a list is totally different from a vector or a deque. Thus, a list differs in several major ways compared with vectors and deques:
A list does not provide random access. For example, to access the fifth element, you must navigate the first four elements following the chain of links. Thus, accessing an arbitrary element using a list is slow.
Inserting and removing elements is fast at each position, and not only at one or both ends. You can always insert and delete an element in constant time because no other elements have to be moved. Internally, only some pointer values are manipulated.
Inserting and deleting elements does not invalidate pointers, references, and iterators to other elements.
A list supports exception handling in such a way that almost every operation succeeds or is a no-op. Thus, you can't get into an intermediate state in which only half of the operation is complete.
The member functions provided for lists reflect these differences compared with vectors and deques as follows:
Lists provide neither a subscript operator nor at() because no random access is provided.
Lists don't provide operations for capacity or reallocation because neither is needed. Each element has its own memory that stays valid until the element is deleted.
Lists provide many special member functions for moving elements. These member functions are faster versions of general algorithms that have the same names. They are faster because they only redirect pointers rather than copy and move the values.
The ability to create, copy, and destroy lists is the same as it is for every sequence container. See Table 6.12 for the list operations that do this. See also Section 6.1.2, for some remarks about possible initialization sources.
| Operation | Effect |
|---|---|
| list<Elem> c | Creates an empty list without any elements |
| list<Elem> c1(c2) | Creates a copy of another list of the same type (all elements are copied) |
| list<Elem> c(n) | Creates a list with n elements that are created by the default constructor |
| list<Elem> c(n,elem) | Creates a list initialized with n copies of element elem |
| list<Elem> c (beg,end) | Creates a list initialized with the elements of the range [beg,end) |
| c.~list<Elem>() | Destroys all elements and frees the memory |
Lists provide the usual operations for size and comparisons. See Table 6.13 for a list and Section 6.1.2, for details.
| Operation | Effect |
|---|---|
| c.size() | Returns the actual number of elements |
| c. empty () | Returns whether the container is empty (equivalent to size()==0, but might be faster) |
| c.max_size() | Returns the maximum number of elements possible |
| c1 == c2 | Returns whether c1 is equal to c2 |
| c1 != c2 | Returns whether c1 is not equal to c2 (equivalent to ! (c1==c2)) |
| c1 < c2 | Returns whether c1 is less than c2 |
| c1 > c2 | Returns whether c1 is greater than c2 (equivalent to c2<c1) |
| c1 <= c2 | Returns whether c1 is less than or equal to c2 (equivalent to ! (c2<c1) ) |
| c1 >= c2 | Returns whether c1 is greater than or equal to c2 (equivalent to ! (c1<c2)) |
Lists also provide the usual assignment operations for sequence containers (Table 6.14).
| Operation | Effect |
|---|---|
| c1 = c2 | Assigns all elements of c2 to c1 |
| c.assign(n,elem) | Assigns n copies of element elem |
| c.assign(beg,end) | Assigns the elements of the range [beg,end) |
| c1.swap(c2) | Swaps the data of c1 and c2 |
| swap(c1,c2) | Same (as global function) |
As usual, the insert operations match the constructors to provide different sources for initialization (see Section 6.1.2, for details).
Because a list does not have random access, it provides only front() and back() for accessing elements directly (Table 6.15).
| Operation | Effect |
|---|---|
| c.front() | Returns the first element (no check whether a first element exists) |
| c.back() | Returns the last element (no check whether a last element exists) |
As usual, these operations do not check whether the container is empty. If the container is empty, calling them results in undefined behavior. Thus, the caller must ensure that the container contains at least one element. For example:
std::list<Elem> coll; // empty! std::cout << coll.front(); // RUNTIME ERRORundefined behavior if (!coll.empty()) { std::cout << coll.back(); // OK }
To access all elements of a list, you must use iterators. Lists provide the usual iterator functions (Table 6.16). However, because a list has no random access, these iterators are only bidirectional. Thus, you can't call algorithms that require random access iterators. All algorithms that manipulate the order of elements a lot (especially sorting algorithms) fall under this category. However, for sorting the elements, lists provide the special member function sort() (see page 245).
| Operation | Effect |
|---|---|
| c.begin() | Returns a bidirectional iterator for the first element |
| c.end() | Returns a bidirectional iterator for the position after the last element |
| c.rbegin() | Returns a reverse iterator for the first element of a reverse iteration |
| c.rend() | Returns a reverse iterator for the position after the last element of a reverse iteration |
Table 6.17 shows the operations provided for lists to insert and to remove elements. Lists provide all functions of deques, supplemented by special implementations of the remove() and remove_if() algorithms.
As usual by using the STL, you must ensure that the arguments are valid. Iterators must refer to valid positions, the beginning of a range must have a position that is not behind the end, and you must not try to remove an element from an empty container.
Inserting and removing happens faster if, when working with multiple elements, you use a single call for all elements rather than multiple calls.
For removing elements, lists provide special implementations of the remove() algorithms (see Section 9.7.1). These member functions are faster than the remove() algorithms because they manipulate only internal pointers rather than the elements. So, in contrast to vectors or deques, you should call remove() as a member function and not as an algorithm (as mentioned on page 154). To remove all elements that have a certain value, you can do the following (see Section 5.6.3, for further details):
std::list<Elem> coll;
...
//remove all elements with value val
coll.remove(val);
| Operation | Effect |
| c.insert (pos, elem) | Inserts at iterator position pos a copy of elem and returns the position of the new element |
| c.insert (pos,n, elem) | Inserts at iterator position pos n copies of elem (returns nothing) |
| c. insert (pos, beg,end) | Inserts at iterator position pos a copy of all elements of the range [beg,end) (returns nothing) |
| c.push_back(elem) | Appends a copy of elem at the end |
| c.pop_back() | Removes the last element (does not return it) |
| c.push_front(elem) | Inserts a copy of elem at the beginning |
| c.pop_front () | Removes the first element (does not return it) |
| c. remove (val) | Removes all elements with value val |
| c.remove_if (op) | Removes all elements for which op(elem) yields true |
| c. erase (pos) | Removes the element at iterator position pos and returns the position of the next element |
| c.erase (beg,end) | Removes all elements of the range [beg,end) and returns the position of the next element |
| c. resize (num) | Changes the number of elements to num (if size() grows, new elements are created by their default constructor) |
| c.resize (num, elem) | Changes the number of elements to num (if size ( ) grows, new elements are copies of elem) |
| c. clear () | Removes all elements (makes the container empty) |
However, to remove only the first occurrence of a value, you must use an algorithm such as that mentioned on page 154 for vectors.
You can use remove_if() to define the criterion for the removal of the elements by a function or a function object.[13] remove_if() removes each element for which calling the passed operation yields true. An example of the use of remove_if() is a statement to remove all elements that have an even value:
list.remove_if (not1(bind2nd(modulus<int>(),2)));
If you don't understand this statement, don't panic. Turn to page 306 for details. See page 378 for additional examples of remove() and remove_if().
Linked lists have the advantage that you can remove and insert elements at any position in constant time. If you move elements from one container to another, this advantage doubles in that you only need to redirect some internal pointers (Figure 6.5).
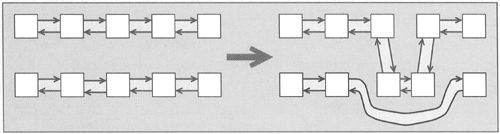
To support this ability, lists provide not only remove() but also additional modifying member functions to change the order of and relink elements and ranges. You can call these operations to move elements inside a single list or between two lists, provided the lists have the same type. Table 6.18 lists these functions. They are covered in detail in Section 6.10.8, with examples in Section 6.4.4.
| Operation | Effect |
| c.unique() | Removes duplicates of consecutive elements with the same value |
| c.unique(op) | Removes duplicates of consecutive elements, for which op() yields true |
| c1.splice(pos,c2) | Moves all elements of c2 to c1 in front of the iterator position pos |
| c1.splice(pos,c2,c2pos) | Moves the element at c2pos in c2 in front of pos of list c1 (c1 and c2 may be identical) |
| c1.splice(pos,c2,c2beg,c2end) | Moves all elements of the range [c2beg,c2end) in c2 in front of pos of list c1 (c1 and c2 may be identical) |
| c.sort() | Sorts all elements with operator < |
| c.sort(op) | Sorts all elements with op() |
| c1.merge(c2) | Assuming both containers contain the elements sorted, moves all elements of c2 into c1 so that all elements are merged and still sorted |
| c1.merge(c2,op) | Assuming both containers contain the elements sorted due to the sorting criterion op(), moves all elements of c2 into c1 so that all elements are merged and still sorted according to op() |
| c.reverse() | Reverses the order of all elements |
Lists have the best support of exception safety of the standard containers in the STL. Almost all list operations will either succeed or have no effect. The only operations that don't give this guarantee in face of exceptions are assignment operations and the member function sort() (they give the usual "basic guarantee" that they will not leak resources or violate container invariants in the face of exceptions), merge(), remove(), remove_if(), and unique() give guarantees under the condition that comparing the elements (using operator == or the predicate) doesn't throw. Thus, to use a term from database programming, you could say that lists are transaction safe, provided you don't call assignment operations or sort() and ensure that comparing elements doesn't throw. Table 6.19 lists all operations that give special guarantees in face of exceptions. See Section 5.11.2, for a general discussion of exception handling in the STL.
| Operation | Guarantee |
| push_back() | Either succeeds or has no effect |
| push_front() | Either succeeds or has no effect |
| insert () | Either succeeds or has no effect |
| pop_back() | Doesn't throw |
| pop_front() | Doesn't throw |
| erase() | Doesn't throw |
| clear() | Doesn't throw |
| resize() | Either succeeds or has no effect |
| remove() | Doesn't throw if comparing the elements doesn't throw |
| remove_if() | Doesn't throw if the predicate doesn't throw |
| Unique() | Doesn't throw if comparing the elements doesn't throw |
| splice() | Doesn't throw |
| Merge() | Either succeeds or has no effect if comparing the elements doesn't throw |
| reverse() | Doesn't throw |
| swap() | Doesn't throw |
The following example in particular shows the use of the special member functions for lists:
// cont/list1.cpp #include <iostream> #include <list> #include <algorithm> using namespace std; void printLists (const list<int>& 11, const list<int>& 12) { cout << "list1: "; copy (l1.begin(), l1.end(), ostream_iterator<int>(cout," ")); cout << endl << "list2: "; copy (12.begin(), 12.end(), ostream_iterator<int>(cout," ")); cout << endl << endl; } int main() { //create two empty lists list<int> list1, list2; //fill both lists with elements for (int i=0; i<6; ++i) { list1.push_back(i); list2.push_front(i); } printLists(list1, list2); //insert all elements of list1 before the first element with value 3 of list2 //-find() returns an iterator to the first element with value 3 list2.splice(find(list2.begin(),list2.end(), // destination position 3), list1); // source list printLists(list1, list2); //move first element to the end list2.splice(list2.end(), // destination position list2, // source list list2.begin()); // source position printLists(list1, list2); //sort second list, assign to list1 and remove duplicates list2.sort(); list1 = list2; list2.unique(); printLists(list1, list2); //merge both sorted lists into the first list list1.merge(list2); printLists(list1, list2); }
The program has the following output:
list1: 0 1 2 3 4 5 list2: 5 4 3 2 1 0 list1: list2: 5 4 0 1 2 3 4 5 3 2 1 0 list1: list2: 4 0 1 2 3 4 5 3 2 1 0 5 list1: 0 0 1 1 2 2 3 3 4 4 5 5 list2: 0 1 2 3 4 5 list1: 0 0 0 1 1 1 2 2 2 3 3 3 4 4 4 5 5 5 list2:
Set and multiset containers sort their elements automatically according to a certain sorting criterion. The difference between the two is that multisets allow duplicates, whereas sets do not (see Figure 6.6 and the earlier discussion on this topic in Chapter 5).
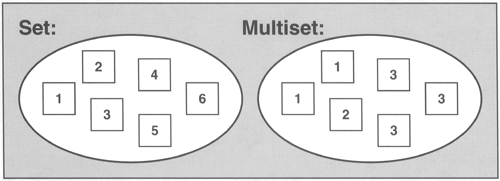
To use a set or multiset, you must include the header file <set>[14]:
#include <set>
There, the type is defined as a template class inside namespace std:
namespace std {
template <class T,
class Compare = less<T>,
class Allocator = allocator<T> >
class set;
template <class T,
class Compare = less<T>,
class Allocator = allocator<T> >
class multiset;
}
The elements of a set or multiset may have any type T that is assignable, copyable, and comparable according to the sorting criterion. The optional second template argument defines the sorting criterion. If a special sorting criterion is not passed, the default criterion less is used. The function object less sorts the elements by comparing them with operator < (see page 305 for details about less).[15] The optional third template parameter defines the memory model (see Chapter 15). The default memory model is the model allocator, which is provided by the C++ standard library.[16]
The sorting criterion must define "strict weak ordering." Strict weak ordering is defined by the following three properties:
It has to be antisymmetric.
This means for operator <: If x < y is true, then y < x is false.
This means for a predicate op(): If op(x,y) is true, then op(y,x) is false.
It has to be transitive.
This means for operator <: If x < y is true and y < z is true, then x < z is true.
This means for a predicate op(): If op(x,y) is true and op (y,z) is true, then op(x,z) is true.
It has to be irreflexive.
This means for operator <:x < x is always false.
This means for a predicate op(): op(x,x) is always false.
Based on these properties the sorting criterion is also used to check equality. That is, two elements are equal if neither is less than the other (or if both op(x,y) and op(y,x) are false).
Like all standardized associative container classes, sets and multisets are usually implemented as balanced binary trees (Figure 6.7). The standard does not specify this, but it follows from the complexity of set and multiset operations.[17]
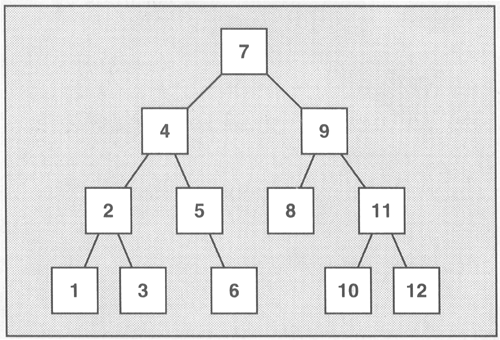
The major advantage of automatic sorting is that a binary tree performs well when elements with a certain value are searched. In fact, search functions have logarithmic complexity. For example, to search for an element in a set or multiset of 1,000 elements, a tree search (which is performed by the member function) needs, on average, one fiftieth of the comparisons of a linear search (which is performed by the algorithm). See Section 2.3, for more details about complexity.
However, automatic sorting also imposes an important constraint on sets and multisets: You may not change the value of an element directly because this might compromise the correct order. Therefore, to modify the value of an element, you must remove the element that has the old value and insert a new element that has the new value. The interface reflects this behavior:
Sets and multisets don't provide operations for direct element access.
Indirect access via iterators has the constraint that, from the iterator's point of view, the element value is constant.
Table 6.20 lists the constructors and destructors of sets and multisets.
| Operation | Effect |
| set c | Creates an empty set/multiset without any elements |
| set c(op) | Creates an empty set/multiset that uses op as the sorting criterion |
| set c1(c2) | Creates a copy of another set/multiset of the same type (all elements are copied) |
| set c(beg,end) | Creates a set/multiset initialized by the elements of the range [beg,end) |
| set c(beg,end, op) | Creates a set/multiset with the sorting criterion op initialized by the elements of the range [beg,end) |
| c.~set() | Destroys all elements and frees the memory |
Here, set may be one of the following:
| set | Effect |
| set<Elem> | A set that sorts with less<> (operator <) |
| set<Elem,0p> | A set that sorts with 0p |
| multiset<Elem> | A multiset that sorts with less<> (operator <) |
| multiset<Elem,0p> | A multiset that sorts with 0p |
You can define the sorting criterion in two ways:
As a template parameter.
For example[18]:
std::set<int,std::greater<int> > coll;
In this case, the sorting criterion is part of the type. Thus, the type system ensures that only containers with the same sorting criterion can be combined. This is the usual way to specify the sorting criterion. To be more precise, the second parameter is the type of the sorting criterion. The concrete sorting criterion is the function object that gets created with the container. To do this, the constructor of the container calls the default constructor of the type of the sorting criterion. See page 294 for an example that uses a user-defined sorting criterion.
As a constructor parameter.
In this case, you might have a type for several sorting criteria, and the initial value or state of the sorting criteria might differ. This is useful when processing the sorting criterion at runtime and when sorting criteria are needed that are different but of the same data type. See page 191 for a complete example.
If no special sorting criterion is passed, the default sorting criterion, function object less<>, is used, which sorts the elements by using operator <.[19]
set<int,less<int> > coll;
Note that the sorting criterion is also used to check for equality of the elements. Thus, when the default sorting criterion is used, the check for equality of two elements looks like this:
if (! (elem1<elem2 || elem2<elem1))
This has three advantages:
You need to pass only one argument as the sorting criterion.
You don't have to provide operator == for the element type.
You can have contrary definitions for equality (it doesn't matter if operator == behaves differently than in the expression). However, this might be a source of confusion.
However, checking for equality in this way takes a bit more time. This is because two comparisons might be necessary to evaluate the previous expression. Note that if the result of the first comparison yields true, the second comparison is not evaluated.
By now the type name of the container might be a bit complicated and boring, so it is probably a good idea to use a type definition. This definition could be used as a shortcut wherever the container type is needed (this also applies to iterator definitions):
typedef std::set<int,std::greater<int> > IntSet; ... IntSet coll; IntSet::iterator pos;
The constructor for the beginning and the end of a range could be used to initialize the container with elements from containers that have other types, from arrays, or from the standard input. See Section 6.1.2, for details.
Sets and multisets provide the usual nonmodifying operations to query the size and to make comparisons (Table 6.21).
| Operation | Effect |
| c.size() | Returns the actual number of elements |
| c.empty () | Returns whether the container is empty (equivalent to size()==0, but might be faster) |
| c.max_size() | Returns the maximum number of elements possible |
| c1 == c2 | Returns whether c1 is equal to c2 |
| c1 != c2 | Returns whether c1 is not equal to c2 (equivalent to ! (c1==c2) ) |
| c1 < c2 | Returns whether c1 is less than c2 |
| c1 > c2 | Returns whether c1 is greater than c2 (equivalent to c2<c1) |
| c1 <= c2 | Returns whether c1 is less than or equal to c2 (equivalent to ! (c2<c1) ) |
| c1 >= c2 | Returns whether c1 is greater than or equal to c2 (equivalent to !(c1<c2)) |
Comparisons are provided only for containers of the same type. Thus, the elements and the sorting criterion must have the same types; otherwise, a type error occurs at compile time. For example:
std::set<float> c1; // sorting criterion: std::less<> std::set<float,std::greater<float> > c2; ... if (c1 == c2) { // ERROR: different types ... }
The check whether a container is less than another container is done by a lexicographical comparison (see page 360). To compare containers of different types (different sorting criteria), you must use the comparing algorithms in Section 9.5.4.
Sets and multisets are optimized for fast searching of elements, so they provide special search functions (Table 6.22). These functions are special versions of general algorithms that have the same name. You should always prefer the optimized versions for sets and multisets to achieve logarithmic complexity instead of the linear complexity of the general algorithms. For example, a search of a collection of 1,000 elements requires on average only 10 comparisons instead of 500 (see Section 2.3,).
| Operation | Effect |
| count (elem) | Returns the number of elements with value elem |
| find(elem) | Returns the position of the first element with value elem or end() |
| lower _bound( elem) | Returns the first position, where elem would get inserted (the first element >= elem) |
| upper _bound (elem) | Returns the last position, where elem would get inserted (the first element > elem) |
| equal_range (elem) | Returns the first and last position, where elem would get inserted (the range of elements == elem) |
The find() member function searches the first element that has the value that was passed as the argument and returns its iterator position. If no such element is found, find() returns end() of the container.
lower_bound() and upper_bound() return the first and last position respectively, at which an element with the passed value would be inserted. In other words, lower_bound() returns the position of the first element that has the same or a greater value than the argument, whereas upper_bound() returns the position of the first element with a greater value. equal_range() returns both return values of lower_bound() and upper_bound() as a pair (type pair is introduced in Section 4.1). Thus, it returns the range of elements that have the same value as the argument. If lower_bound() or the first value of equal_range() is equal to upper_bound() or the second value of equal_range(), then no elements with the same value exist in the set or multiset. Naturally, in a set the range of elements that have the same values could contain at most one element.
The following example shows how to use lower_bound(), upper_bound(), and equal_range():
// cont/set2.cpp
#include <iostream>
#include <set>
using namespace std;
int main ()
{
set<int> c;
c.insert(1);
c.insert(2);
c.insert(4);
c.insert(5);
c.insert(6);
cout << "lower_bound(3): " << *c.lower_bound(3) << endl;
cout << "upper_bound(3): " << *c.upper_bound(3) << endl;
cout << "equal_range(3): " << *c.equal_range(3).first << " "
<< *c.equal_range(3).second << endl;
cout << endl;
cout << "lower_bound(5): " << *c.lower_bound(5) << endl;
cout << "upper_bound(5): " << *c.upper_bound(5) << endl;
cout << "equal_range(5): " << *c.equal_range(5).first << " "
<< *c.equal_range(5).second << endl;
}
The output of the program is as follows:
lower_bound(3): 4
upper_bound(3): 4
equal_range(3): 4 4
lower_bound(5): 5
upper_bound(5): 6
equal_range(5): 5 6
If you use a multiset instead of a set, the program has the same output.
Sets and multisets provide only the fundamental assignment operations that all containers provide (Table 6.23). See page 147 for more details.
For these operations both containers must have the same type. In particular, the type of the comparison criteria must be the same, although the comparison criteria themselves may be different. See page 191 for an example of different sorting criteria that have the same type. If the criteria are different, they will also get assigned or swapped.
| Operation | Effect |
| c1 = c2 | Assigns all elements of c2 to c1 |
| c1.swap(c2) | Swaps the data of c1 and c2 |
| swap(c1,c2) | Same (as global function) |
Sets and multisets do not provide direct element access, so you have to use iterators. Sets and multisets provide the usual member functions for iterators (Table 6.24).
| Operation | Effect |
| c.begin() | Returns a bidirectional iterator for the first element (elements are considered const) |
| c.end() | Returns a bidirectional iterator for the position after the last element (elements are considered const) |
| c.rbegin() | Returns a reverse iterator for the first element of a reverse iteration |
| c.rend() | Returns a reverse iterator for the position after the last element of a reverse iteration |
As with all associative container classes, the iterators are bidirectional iterators (see Section 7.2.4). Thus, you can't use them in algorithms that are provided only for random access iterators (such as algorithms for sorting or random shuffling).
More important is the constraint that, from an iterator's point of view, all elements are considered constant. This is necessary to ensure that you can't compromise the order of the elements by changing their values. However, as a result you can't call any modifying algorithm on the elements of a set or multiset. For example, you can't call the remove() algorithm to remove elements because it "removes" by overwriting "removed" elements the with following arguments (see Section 5.6.2, for a detailed discussion of this problem). To remove elements in sets and multisets, you can use only member functions provided by the container.
Table 6.25 shows the operations provided for sets and multisets to insert and remove elements.
As usual by using the STL, you must ensure that the arguments are valid. Iterators must refer to valid positions, the beginning of a range must have a position that is not behind the end, and you must not try to remove an element from an empty container.
Inserting and removing happens faster if, when working with multiple elements, you use a single call for all elements rather than multiple calls.
| Operation | Effect |
| c. insert(elem) | Inserts a copy of elem and returns the position of the new element and, for sets, whether it succeeded |
| c. insert(pos, elem) | Inserts a copy of elem and returns the position of the new element (pos is used as a hint pointing to where the insert should start the search) |
| c. insert (beg,end) | Inserts a copy of all elements of the range [beg,end) (returns nothing) |
| c. erase(elem) | Removes all elements with value elem and returns the number of removed elements |
| c. erase(pos) | Removes the element at iterator position pos (returns nothing) |
| c. erase(beg,end) | Removes all elements of the range [beg,end) (returns nothing) |
| c. clear() | Removes all elements (makes the container empty) |
Note that the return types of the insert functions differ as follows:
Sets provide the following interface:
pair<iterator,bool> insert(const value_type& elem);
iterator insert(iterator pos_hint,
const value_type& elem);
Multisets provide the following interface:
iterator insert(const value_type& elem);
iterator insert(iterator pos_hint,
const value_type& elem);
The difference in return types results because multisets allows duplicates, whereas sets do not. Thus, the insertion of an element might fail for a set if it already contains an element with the same value. Therefore, the return type of a set returns two values by using a pair structure (pair is discussed in Section 4.1,):
The member second of the pair structure returns whether the insertion was successful.
The member first of the pair structure returns the position of the newly inserted element or the position of the still existing element.
In all other cases, the functions return the position of the new element (or of the existing element if the set contains an element with the same value already).
The following example shows how to use this interface to insert a new element into a set. It tries to insert the element with value 3.3 into the set c:
std::set<double> c;
if (c.insert(3.3).second) {
std::cout << "3.3 inserted" << std::endl;
}
else {
std::cout << "3.3 already exists" << std::endl;
}
If you also want to process the new or old positions, the code gets more complicated:
//define variable for return value of insert() std::pair<std::set<float>::iterator,bool> status; //insert value and assign return value status = c.insert(value); //process return value if (status.second) { std::cout << value << " inserted as element " } else { std::cout << value << " already exists as element " } std::cout << std::distance(c.begin().status.first) + 1 << std::endl;
The output of two calls of this sequence might be as follows:
8.9 inserted as element 4 7.7 already exists as element 3
Note that the return types of the insert functions with an additional position parameter don't differ. These functions return a single iterator for both sets and multisets. However, these functions have the same effect as the functions without the position parameter. They differ only in their performance. You can pass an iterator position, but this position is processed as a hint to optimize performance. In fact, if the element gets inserted right after the position that is passed as the first argument, the time complexity changes from logarithmic to amortized constant (complexity is discussed in Section 2.3,). The fact that the return type for the insert functions with the additional position hint doesn't have the same difference as the insert functions without the position hint ensures that you have one insert function that has the same interface for all container types. In fact, this interface is used by general inserters. See Section 7.4.2, especially page 275, for details about inserters. To remove an element that has a certain value, you simply call erase():
std::set<Elem> coll;
...
//remove all elements with passed value
coll.erase(value);
Unlike with lists, the erase() member function does not have the name remove() (see page 170 for a discussion of remove()). It behaves differently because it returns the number of removed elements. When called for sets, it returns only 0 or 1.
If a multiset contains duplicates, you can't use erase() to remove only the first element of these duplicates. Instead, you can code as follows:
std::multiset<Elem> coll;
...
//remove first element with passed value
std::multiset<Elem>::iterator pos;
pos = coll.find (elem);
if (pos != coll.end()) {
coll.erase(pos);
}
You should use the member function find() instead of the find() algorithm here because it is faster (see the example on page 154).
Note that there is another inconsistency in return types here. That is, the return types of the erase() functions differ between sequence and associative containers as follows:
Sequence containers provide the following erase() member functions:
iterator erase(iterator pos);
iterator erase(iterator beg, iterator end);
Associative containers provide the following erase() member functions:
void erase(iterator pos);
void erase(iterator beg, iterator end);
The reason for this difference is performance. It might cost time to find and return the successor in an associative container because the container is implemented as a binary tree. However, as a result, to write generic code for all containers you must ignore the return value.
Sets and multisets are node-based containers, so any failure to construct a node simply leaves the container as it was. Furthermore, because destructors in general don't throw, removing a node can't fail.
However, for multiple-element insert operations, the need to keep elements sorted makes full recovery from throws impractical. Thus, all single-element insert operations support commit-or-rollback behavior. That is, they either succeed or they have no effect. In addition, it is guaranteed that all multiple-element delete operations always succeed. If copying/assigning the comparison criterion may throw, swap() may throw.
See Section 5.11.2, for a general discussion of exceptions handling in the STL and Section 6.10.10, for a list of all container operations that give special guarantees in face of exceptions.
The following program demonstrates some abilities of sets[20]:
// cont/set1.cpp #include <iostream> #include <set> using namespace std; int main() { /*type of the collection: *-no duplicates *-elements are integral values *-descending order */ typedef set<int,greater<int> > IntSet; IntSet coll1; // empty set container //insert elements in random order coll1.insert(4); coll1.insert(3); coll1.insert(5); coll1.insert(1); coll1.insert(6); coll1.insert(2); coll1.insert(5); //iterate over all elements and print them IntSet::iterator pos; for (pos = coll1.begin(); pos != coll1.end(); ++pos) { cout << *pos << ' '; } cout << endl; //insert 4 again and process return value pair<IntSet::iterator,bool> status = coll1.insert(4); if (status.second) { cout << "4 inserted as element " << distance (coll1.begin(),status. first) + 1 << endl; } else { cout << "4 already exists" << endl; } //assign elements to another set with ascending order set<int> coll2(coll1.begin(), coll1.end()); //print all elements of the copy copy (coll2.begin(), coll2.end(), ostream_iterator<int>(cout," ")); cout << endl; //remove all elements up to element with value 3 coll2.erase (coll2.begin(), coll2.find(3)); //remove all elements with value 5 int num; num = coll2.erase (5); cout << num << " element(s) removed" << endl; //print all elements copy (coll2.begin(), coll2.end(), ostream_iterator<int>(cout," ")); cout << endl; }
At first, the type definition
typedef set<int,greater<int> > IntSet;
defines a short type name for a set of ints with descending order. After an empty set is created, several elements are inserted by using insert ():
IntSet coll1; coll1.insert(4); ...
Note that the element with value 5 is inserted twice. However, the second insertion is ignored because sets do not allow duplicates.
After printing all elements, the program tries again to insert the element 4. This time it processes the return values of insert() as discussed on page 183.
The statement
set<int> coll2(coll1.begin(), coll1. end());
creates a new set of ints with ascending order and initializes it with the elements of the old set.[21]
set<int,less<int> > coll2;
copy (coll1.begin(), coll1. end(),
inserter(coll2,coll2.begin()));
Both containers have different sorting criteria, so their types differ and you can't assign or compare them directly. However, you can use algorithms, which in general are able to handle different container types as long as the element types are equal or convertible.
The statement
coll2.erase (coll2.begin(), coll2.find(3));
removes all elements up to the element with value 3. Note that the element with value 3 is the end of the range, so that it is not removed.
Lastly, all elements with value 5 are removed:
int num; num = coll2.erase (5); cout << num << " element(s) removed" << endl;
The output of the whole program is as follows:
6 5 4 3 2 1 4 already exists 1 2 3 4 5 6 1 element(s) removed 3 4 6
For multisets, the same program looks a bit differently and produces different results:
// cont/mset1.cpp #include <iostream> #include <set> using namespace std; int main() { /*type of the collection: *-duplicates allowed *-elements are integral values *-descending order */ typedef multiset<int,greater<int> > IntSet; IntSet coll1, // empty multiset container //insert elements in random order coll1.insert(4); coll1.insert(3); coll1.insert(5); coll1.insert(l); coll1.insert(6); coll1.insert(2); coll1.insert(5); //iterate over all elements and print them IntSet::iterator pos; for (pos = coll1.begin(); pos != coll1.end(); ++pos) { cout << *pos << ' '; } cout << endl; //insert 4 again and process return value IntSet::iterator ipos = coll1.insert(4); cout << "4 inserted as element " << distance (coll1.begin(),ipos) + 1 << endl; //assign elements to another multiset with ascending order multiset<int> coll2(coll1.begin(), coll1.end()); //print all elements of the copy copy (coll2.begin(), coll2.end(), ostream_iterator<int>(cout," ")); cout << endl; //remove all elements up to element with value 3 coll2.erase (coll2.begin(), coll2.find(3)); //remove all elements with value 5 int num; num = coll2.erase (5); cout << num << " element(s) removed" << endl; //print all elements copy (coll2.begin(), coll2.end(), ostream_iterator<int>(cout," ")); cout << endl; }
In all cases type set was changed to multiset. In addition, the processing of the return value of insert() looks different:
IntSet::iterator ipos = coll1.insert(4);
cout << "4 inserted as element "
<< distance (coll1.begin(),ipos) + 1
<< endl;
Because multisets may contain duplicates, the insertion can fail only if an exception gets thrown. Thus, the return type is only the iterator position of the new element.
The output of the program changed as follows:
6 5 5 4 3 2 1 4 inserted as element 5 1 2 3 4 4 5 5 6 2 element(s) removed 3 4 4 6
Normally you define the sorting criterion as part of the type, either by passing it as a second template argument or by using the default sorting criterion less<>. However, sometimes you must process the sorting criterion at runtime, or you may need different sorting criteria with the same data type. In this case, you need a special type for the sorting criterion — one that lets you pass your sorting details at runtime. The following example program demonstrates how to do this:
// cont/setcmp.cpp #include <iostream> #include <set> #include "print.hpp" using namespace std; //type for sorting criterion template <class T> class RuntimeCmp { public: enum cmp_mode {normal, reverse}; private: cmp_mode mode; public: //constructor for sorting criterion //-default criterion uses value normal RuntimeCmp (cmp_mode m=normal) : mode(m) { } //comparision of elements bool operator() (const T& t1, const T& t2) const { return mode == normal ? t1 < t2 : t2 < t1; } //comparision of sorting criteria bool operator== (const RuntimeCmp& rc) { return mode == rc.mode; } }; //type of a set that uses this sorting criterion typedef set<int,RuntimeCmp<int> > IntSet; //forward declaration void fill (IntSet& set); int main() { //create, fill, and print set with normal element order //-uses default sorting criterion IntSet coll1; fill(coll1); PRINT_ELEMENTS (coll1, "coll1: "); //create sorting criterion with reverse element order RuntimeCmp<int> reverse_order(RuntimeCmp<int>::reverse); //create, fill, and print set with reverse element order IntSet coll2(reverse_order); fill(coll2); PRINT_ELEMENTS (coll2, "coll2: "); //assign elements AND sorting criterion coll1 = coll2; coll1.insert(3); PRINT_ELEMENTS (coll1, "coll1: "); //just to make sure... if (coll1.value_comp() == coll2.value_comp()) { cout << "coll1 and coll2 have same sorting criterion" << endl; } else { cout << "coll1 and coll2 have different sorting criterion" << endl; } } void fill (IntSet& set) { //fill insert elements in random order set.insert(4); set.insert(7); set.insert(5); set.insert(1); set.insert(6); set.insert(2); set.insert(5); }
In this program, RuntimeCmp<> is a simple template that provides the general ability to specify, at runtime, the sorting criterion for any type. Its default constructor sorts in ascending order using the default value normal. It also is possible to pass RuntimeCmp<>::reverse to sort in descending order.
The output of the program is as follows:
coll1: 1 2 4 5 6 7 coll2: 7 6 5 4 2 1 coll1: 7 6 5 4 3 2 1 coll1 and coll2 have same sorting criterion
Note that coll1 and coll2 have the same type, which is used in fill(), for example. Note also that the assignment operator assigns the elements and the sorting criterion (otherwise an assignment would be an easy way to compromise the sorting criterion).
Map and multimap containers are containers that manage key/value pairs as elements. They sort their elements automatically according to a certain sorting criterion that is used for the actual key. The difference between the two is that multimaps allow duplicates, whereas maps do not (Figure 6.8).

To use a map or multimap, you must include the header file <map>[22]:
#include <map>
There, the type is defined as a class template inside namespace std:
namespace std {
template <class Key, class T,
class Compare = less<Key>,
class Allocator = allocator<pair<const Key,T> > >
class map;
template <class Key, class T,
class Compare = less<Key>,
class Allocator = allocator<pair<const Key,T> > >
class multimap;
}
The first template argument is the type of the element's key, and the second template argument is the type of the element's value. The elements of a map or multimap may have any types Key and T that meet the following two requirements:
The key/value pair must be assignable and copyable.
The key must be comparable with the sorting criterion.
The optional third template argument defines the sorting criterion. Like sets, this sorting criterion must define a "strict weak ordering" (see page 176). The elements are sorted according to their keys, thus the value doesn't matter for the order of the elements. The sorting criterion is also used to check equality; that is, two elements are equal if neither key is less than the other. If a special sorting criterion is not passed, the default criterion less is used. The function object less sorts the elements by comparing them with operator < (see page 305 for details about less).[23]
The optional fourth template parameter defines the memory model (see Chapter 15). The default memory model is the model allocator, which is provided by the C++ standard library.[24]
Like all standardized associative container classes, maps and multimaps are usually implemented as balanced binary trees (Figure 6.9). The standard does not specify this but it follows from the complexity of the map and multimap operations. In fact, sets, multisets, maps, and multimaps typically use the same internal data type. So, you could consider sets and multisets as special maps and multimaps, respectively, for which the value and the key of the elements are the same objects. Thus, maps and multimaps have all the abilities and operations of sets and multisets. Some minor differences exist, however. First, their elements are key/value pairs. In addition, maps can be used as associative arrays.
Maps and multimaps sort their elements automatically according to the element's keys. Thus they have good performance when searching for elements that have a certain key. Searching for elements that have a certain value promotes bad performance. Automatic sorting imposes an important constraint on maps and multimaps: You may not change the key of an element directly because this might compromise the correct order. To modify the key of an element, you must remove the element that has the old key and insert a new element that has the new key and the old value (see page 201 for details). As a consequence, from the iterator's point of view, the element's key is constant. However, a direct modification of the value of the element is still possible (provided the type of the value is not constant).
Table 6.26 lists the constructors and destructors of maps and multimaps.
| Operation | Effect |
| map c | Creates an empty map/multimap without any elements |
| map c(op) | Creates an empty map/multimap that uses op as the sorting criterion |
| map c1(c2) | Creates a copy of another map/multimap of the same type (all elements are copied) |
| map c(beg,end) | Creates a map/multimap initialized by the elements of the range [beg,end) |
| map c(beg,end,op) | Creates a map/multimap with the sorting criterion op initialized by the elements of the range [beg,end) |
| c. ~map () | Destroys all elements and frees the memory |
Here, map may be one of the following:
| Map | Effect |
| map<Key,Elem> | A map that sorts keys with less<> (operator <) |
| map<Key,Elem,Op> | A map that sorts keys with Op |
| multimap<Key,Elem> | A multimap that sorts keys with less<> (operator <) |
| multimap<Key,Elem,Op> | A multimap that sorts keys with Op |
You can define the sorting criterion in two ways:
As a template parameter.
For example[25]:
std::map<float,std::string,std::greater<float> > coll;
In this case, the sorting criterion is part of the type. Thus, the type system ensures that only containers with the same sorting criterion can be combined. This is the usual way to specify the sorting criterion. To be more precise, the third parameter is the type of the sorting criterion. The concrete sorting criterion is the function object that gets created with the container. To do this, the constructor of the container calls the default constructor of the type of the sorting criterion. See page 294 for an example that uses a user-defined sorting criterion.
As a constructor parameter.
In this case you might have a type for several sorting criteria, and the initial value or state of the sorting criteria might differ. This is useful when processing the sorting criterion at runtime, or when sorting criteria are needed that are different but of the same data type. A typical example is specifying the sorting criterion for string keys at runtime. See page 213 for a complete example.
If no special sorting criterion is passed, the default sorting criterion, function object less<>, is used. which sorts the elements by using operator <.[26]
map<float,string,less<float> > coll;
You should make a type definition to avoid the boring repetition of the type whenever it is used:
typedef std::map<std::string,float,std::greater<string> >
StringFloatMap;
...
StringFloatMap coll;
The constructor for the beginning and the end of a range could be used to initialize the container with elements from containers that have other types, from arrays, or from the standard input. See Section 6.1.2, for details. However, the elements are key/value pairs, so you must ensure that the elements from the source range have or are convertible into type pair<key,value>.
Maps and multimaps provide the usual nonmodifying operations — those that query size aspects and make comparisons (Table 6.27).
| Operation | Effect |
| c.size() | Returns the actual number of elements |
| c.empty() | Returns whether the container is empty (equivalent to size()==0, but might be faster) |
| c.max_size() | Returns the maximum number of elements possible |
| c1 == c2 | Returns whether c1 is equal to c2 |
| c1 != c2 | Returns whether c1 is not equal to c2 (equivalent to !(c1==c2)) |
| c1 < c2 | Returns whether c1 is less than c2 |
| c1 > c2 | Returns whether c1 is greater than c2 c2<c1) |
| c1 <= c2 | Returns whether c1 is less than or equal to c2 (equivalent to !(c2<c1)) |
| c1 >= c2 | Returns whether c1 is greater than or equal to c2 (equivalent to !(c1<c2)) |
Comparisons are provided only for containers of the same type. Thus, the key, the value, and the sorting criterion must be of the same type. Otherwise, a type error occurs at compile time. For example:
std::map<float,std::string> c1; // sorting criterion: less<> std::map<float,std::string,std::greater<float> > c2; ... if (c1 == c2) { // ERROR: different types ... }
To check whether a container is less than another container is done by a lexicographical comparison (see page 360). To compare containers of different types (different sorting criterion), you must use the comparing algorithms of Section 9.5.4.
Like sets and multisets, maps and multimaps provide special search member functions that perform better because of their internal tree structure (Table 6.28).
The find() member function searches for the first element that has the appropriate key and returns its iterator position. If no such element is found, find() returns end() of the container. You can't use the find() member function to search for an element that has a certain value. Instead, you have to use a general algorithm such as the find_if() algorithm, or program an explicit loop. Here is an example of a simple loop that does something with each element that has a certain value:
std::multimap<std::string,float> coll;
...
//do something with all elements having a certain value
std::multimap<std::string,float>::iterator pos;
for (pos = coll.begin(); pos != coll.end(); ++pos) {
if (pos->second == value) {
do_something();
}
}
| Operation | Effect |
| count(key) | Returns the number of elements with key key |
| find(key) | Returns the position of the first element with key key or end() |
| lower_bound(key) | Returns the first position where an element with key key would get inserted (the first element with key >= key) |
| upper_bound(key) | Returns the last position where an element with key key would get inserted (the first element with key > key) |
| equal_range(key) | Returns the first and last positions where elements with key key would get inserted (the range of elements with key == key) |
Be careful when you want to use such a loop to remove elements. It might happen that you saw off the branch on which you are sitting. See page 204 for details about this issue.
Using the find_if() algorithm to search for an element that has a certain value is even more complicated than writing a loop because you have to provide a function object that compares the value of an element with a certain value. See page 211 for an example.
The lower_bound(), upper_bound(), and equal_range() functions behave as they do for sets (see page 180), except that the elements are key/value pairs.
Maps and multimaps provide only the fundamental assignment operations that all containers provide (Table 6.29). See page 147 for more details.
| Operation | Effect |
| c1 = c2 | Assigns all elements of c2 c1 |
| c1.swap(c2) | Swaps the data of c1 and c2 |
| swap(c1,c2) | Same (as global function) |
For these operations both containers must have the same type. In particular, the type of the comparison criteria must be the same, although the comparison criteria themselves may be different. See page 213 for an example of different sorting criteria that have the same type. If the criteria are different, they also get assigned or swapped.
Maps and multimaps do not provide direct element access, so the usual way to access elements is via iterators. An exception to that rule is that maps provide the subscript operator to access elements directly. This is covered in Section 6.6.3. Table 6.30 lists the usual member functions for iterators that maps and multimaps provide.
| Operation | Effect |
| c.begin() | Returns a bidirectional iterator for the first element (keys are considered const) |
| c.end() | Returns a bidirectional iterator for the position after the last element (keys are considered const) |
| c.rbegin() | Returns a reverse iterator for the first element of a reverse iteration |
| c.rend() | Returns a reverse iterator for the position after the last element of a reverse iteration |
As for all associative container classes, the iterators are bidirectional (see Section 7.2.4, ). Thus, you can't use them in algorithms that are provided only for random access iterators (such as algorithms for sorting or random shuffling).
More important is the constraint that the key of all elements inside a map and a multimap is considered to be constant. Thus, the type of the elements is pair<const Key, T>. This is also necessary to ensure that you can't compromise the order of the elements by changing their keys. However, you can't call any modifying algorithm if the destination is a map or multimap. For example, you can't call the remove() algorithm to remove elements because it "removes" only by overwriting "removed" elements with the following arguments (see Section 5.6.2, for a detailed discussion of this problem). To remove elements in maps and multimaps, you can use only member functions provided by the container.
The following is an example of the use of iterators:
std::map<std::string,float> coll;
...
std::map<std::string,float>::iterator pos;
for (pos = coll.begin(); pos != coll.end(); ++pos) {
std::cout << "key: " << pos->first << "\t"
<< "value: " << pos->second << std::endl;
}
Here, the iterator pos iterates through the sequence of string/float pairs. The expression
pos->first
yields the key of the actual element, whereas the expression
pos->second
yields the value of the actual element.[27]
Trying to change the value of the key results in an error:
pos->first = "hello"; // ERROR at compile time
However, changing the value of the element is no problem (as long as the type of the value is not constant):
pos->second = 13.5; // OK
To change the key of an element, you have only one choice: You must replace the old element with a new element that has the same value. Here is a generic function that does this:
// cont/newkey.hpp namespace MyLib { template <class Cont> inline bool replace_key (Cont& c, const typename Cont::key_type& old_key, const typename Cont::key_type& new_key) { typename Cont::iterator pos; pos = c.find(old_key); if (pos != c.end()) { //insert new element with value of old element c.insert(typename Cont::value_type(new_key, pos->second)); //remove old element c.erase(pos); return true; } else { //key not found return false; } } }
The insert() and erase() member functions are discussed in the next subsection.
To use this generic function you simply must pass the container the old key and the new key. For example:
std::map<std::string,float> coll; ... MyLib::replace_key(coll,"old key","new key");
It works the same way for multimaps.
Note that maps provide a more convenient way to modify the key of an element. Instead of calling replace_key(), you can simply write the following:
//insert new element with value of old element coll["new_key"] = coll["old_key"]; //remove old element coll.erase("old_key");
See Section 6.6.3, for details about the use of the subscript operator with maps.
Table 6.31 shows the operations provided for maps and multimaps to insert and remove elements.
| Operation | Effect |
| c.insert(elem) | Inserts a copy of elem and returns the position of the new element and, for maps, whether it succeeded |
| c.insert(pos,elem) | Inserts a copy of elem and returns the position of the new element (pos is used as a hint pointing to where the insert should start the search) |
| c.insert(beg,end) | Inserts a copy of all elements of the range [beg,end)(returns nothing) |
| c.erase(elem) | Removes all elements with value elem and returns the number of removed elements |
| c.erase(pos) | Removes the element at iterator position pos (returns nothing) |
| c.erase(beg,end) | Removes all elements of the range [beg,end)(returns nothing) |
| c.clear() | Removes all elements (makes the container empty) |
The remarks on page 182 regarding sets and multisets apply here. In particular, the return types of these operations have the same differences as they do for sets and multisets. However, note that the elements here are key/value pairs. So, the use is getting a bit more complicated.
To insert a key/value pair, you must keep in mind that inside maps and multimaps the key is considered to be constant. You either must provide the correct type or you need to provide implicit or explicit type conversions. There are three different ways to pass a value into a map:
Use value_type
To avoid implicit type conversion, you could pass the correct type explicitly by using value_type, which is provided as a type definition by the container type. For example:
std::map<std::string,float> coll;
...
coll.insert(std::map<std::string,float>::value_type("otto",
22.3));
Use pair<>
Another way is to use pair<> directly. For example:
std::map<std::string,float> coll; ... //use implicit conversion: coll.insert(std::pair<std::string,float>("otto",22.3)); //use no implicit conversion: coll.insert(std::pair<const std::string,float>("otto",22.3));
In the first insert() statement the type is not quite right, so it is converted into the real element type. For this to happen, the insert() member function is defined as a member template.[28]
Use make_pair()
Probably the most convenient way is to use the make_pair() function (see page 36). This function produces a pair object that contains the two values passed as arguments:
std::map<std::string,float> coll;
...
coll.insert(std::make_pair("otto",22.3));
Again, the necessary type conversions are performed by the insert() member template.
Here is a simple example of the insertion of an element into a map that also checks whether the insertion was successful:
std::map<std::string,float> coll;
...
if (coll.insert(std::make_pair("otto",22.3)).second) {
std::cout << "OK, could insert otto/22.3" << std::endl;
}
else {
std::cout << "Oops, could not insert otto/22.3 "
<< "(key otto already exists)" << std::endl;
}
See page 182 for a discussion regarding the return values of the insert() functions and more examples that also apply to maps. Note, again, that maps provide a more convenient way to insert (and set) elements with the subscript operator. This is discussed in Section 6.6.3.
To remove an element that has a certain value, you simply call erase():
std::map<std::string,float> coll;
...
//remove all elements with the passed key
coll.erase(key);
This version of erase() returns the number of removed elements. When called for maps, the return value of erase() can only be 0 or 1.
If a multimap contains duplicates, you can't use erase() to remove only the first element of these duplicates. Instead, you could code as follows:
typedef multimap<string.float> StringFloatMMap;
StringFloatMMap coll;
...
//remove first element with passed key
StringFloatMMap::iterator pos;
pos = coll.find(key);
if (pos != coll.end()) {
coll.erase(pos);
}
You should use the member function find() instead of the find() algorithm here because it is faster (see an example with the find() algorithm on page 154). However, you can't use the find() member functions to remove elements that have a certain value (instead of a certain key). See page 198 for a detailed discussion of this topic.
When removing elements, be careful not to saw off the branch on which you are sitting. There is a big danger that will you remove an element to which your iterator is referring. For example:
typedef std::map<std::string,float> StringFloatMap;
StringFloatMap coll;
StringFloatMap::iterator pos;
...
for (pos = coll.begin(); pos != coll.end(); ++pos) {
if (pos->second == value) {
coll. erase (pos); // RUNTIME ERROR !!!
}
}
Calling erase() for the element to which you are referring with pos invalidates pos as an iterator of coll. Thus, if you use pos after removing its element without any reinitialization, then all bets are off. In fact, calling ++pos results in undefined behavior.
A solution would be easy if erase() always returned the value of the following element:
typedef std::map<std::string,float> StringFloatMap;
StringFloatMap coll;
StringFloatMap::iterator pos;
...
for (pos = coll.begin(); pos != coll.end(); ) {
if (pos->second == value) {
pos = coll.erase(pos); // would be fine, but COMPILE TIME ERROR
}
else {
++pos;
}
}
It was a design decision not to provide this trait, because if not needed, it costs unnecessary time. I don't agree with this decision however, because code is getting more error prone and complicated (and may cost even more in terms of time).
Here is an example of the correct way to remove elements to which an iterator refers:
typedef std::map<std::string,float> StringFloatMap;
StringFloatMap coll;
StringFloatMap::iterator pos, tmp_pos;
...
//remove all elements having a certain value
for (pos = c.begin(); pos != c.end(); ) {
if (pos->second == value) {
c.erase(pos++);
}
else {
++pos;
}
}
Note that pos++ increments pos so that it refers to the next element but yields a copy of its original value. Thus, pos doesn't refer to the element that is removed when erase() is called.
Associative containers don't typically provide abilities for direct element access. Instead, you must use iterators. For maps, however, there is an exception to this rule. Nonconstant maps provide a subscript operator for direct element access (Table 6.32). However, the index of the subscript operator is not the integral position of the element. Instead, it is the key that is used to identify the element. This means that the index may have any type rather than only an integral type. Such an interface is the interface of a so-called associative array.
| Operation | Effect |
| m[key] | Returns a reference to the value of the element with key key Inserts an element with key if it does not yet exist |
The type of the index is not the only difference from ordinary arrays. In addition, you can't have a wrong index. If you use a key as the index, for which no element yet exists, a new element gets inserted into the map automatically. The value of the new element is initialized by the default constructor of its type. Thus, to use this feature you can't use a value type that has no default constructor. Note that the fundamental data types provide a default constructor that initializes their values to zero (see page 14).
This behavior of an associative array has both advantages and disadvantages:
The advantage is that you can insert new elements into a map with a more convenient interface.
For example:
std::map<std::string,float> coll; // empty collection /*insert "otto"/7.7 as key/value pair *-first it inserts "otto"/float() *-then it assigns 7.7 */ coll["otto"] = 7.7;
The statement
coll["otto"] = 7.7;
is processed here as follows: Process coll["otto"] expression: If an element with key "otto" exists, the
expression returns the value of the element by reference. If, as in this example, no element with key "otto"
exists, the expression inserts a new element automatically with "otto"
as key and the value of the default constructor of the value type as the
element value. It then returns a reference to that new value of the new
element. Assign value 7.7: The second part of the statement assigns 7.7
to the value of the new or existing element.
The map then contains an element with key "otto" and value 7.7.
The disadvantage is that you might insert new elements by accident or mistake. For example, the following statement does something you probably hadn't intended or expected:
std::cout << coll ["ottto"];
It inserts a new element with key "ottto" and prints its value, which is 0 by default. However, it should have generated an error message telling you that you wrote "otto" incorrectly.
Note, too, that this way of inserting elements is slower than the usual way for maps, which is described on page 202. This is because the new value is first initialized by the default value of its type, which is then overwritten by the correct value.
Maps and multimaps provide the same behavior as sets and multisets with respect to exception safety. This behavior is mentioned on page 185.
The following example shows the use of a map as an associative array. The map is used as a stock chart. The elements of the map are pairs in which the key is the name of the stock and the value is its price:
// cont/mapl.cpp #include <iostream> #include <map> #include <string> using namespace std; int main() { /*create map/associative array *-keys are strings *-values are floats */ typedef map<string,float> StringFloatMap; StringFloatMap stocks; // create empty container //insert some elements stocks["BASF"] = 369.50; stocks["VW"] = 413.50; stocks["Daimler"] = 819.00; stocks["BMW"] = 834.00; stocks["Siemens"] = 842.20; //print all elements StringFloatMap::iterator pos; for (pos = stocks.begin(); pos != stocks.end(); ++pos) { cout << "stock: " << pos->first << "\t" << "price: " << pos->second << endl; } cout << endl; //boom (all prices doubled) for (pos = stocks.begin(); pos != stocks.end(); ++pos) { pos->second *= 2; } //print all elements for (pos = stocks.begin(); pos != stocks.end(); ++pos) { cout << "stock: " << pos->first << "\t" << "price: " << pos->second << endl; } cout << endl; /*rename key from "VW" to "Volkswagen" *-only provided by exchanging element */ stocks["Volkswagen"] = stocks["VW"]; stocks.erase("VW"); //print all elements for (pos = stocks.begin(); pos != stocks.end(); ++pos) { cout << "stock: " << pos->first << "\t" << "price: " << pos->second << endl; } }
The program has the following output:
stock: BASF price: 369.5 stock: BMW price: 834 stock: Daimler price: 819 stock: Siemens price: 842.2 stock: VW price: 413.5 stock: BASF price: 739 stock: BMW price: 1668 stock: Daimler price: 1638 stock: Siemens price: 1684.4 stock: VW price: 827 stock: BASF price: 739 stock: BMW price: 1668 stock: Daimler price: 1638 stock: Siemens price: 1684.4 stock: Volkswagen price: 827
The following example shows how to use a multimap as a dictionary:
// cont/mmap1.cpp #include <iostream> #include <map> #include <string> #include <iomanip> using namespace std; int main() { //define multimap type as string/string dictionary typedef multimap<string,string> StrStrMMap; //create empty dictionary StrStrMMap dict; //insert some elements in random order dict.insert(make_pair("day","Tag")); dict.insert(make_pair("strange","fremd")); dict.insert(make_pair("car","Auto")); dict.insert(make_pair("smart","elegant")); dict.insert(make_pair("trait","Merkmal")); dict.insert(make_pair("strange","seltsam")); dict.insert(make_pair("smart","raffiniert")); dict.insert(make_pair("smart","klug")); dict.insert(make_pair("clever","raffiniert")); //print all elements StrStrMMap::iterator pos; cout.setf (ios::left, ios::adjustfield); cout << ' ' << setw(10) << "english " << "german " << endl; cout << setfil('-') << setw(20) << "" << setfil(' ') << endl; for (pos = dict.begin(); pos != dict.end(); ++pos) { cout << ' ' << setw(10) << pos>first.c_str() << pos->second << endl; } cout << endl; //print all values for key "smart" string word("smart"); cout << word << ": " << endl; for (pos = dict.lower_bound(word); pos != dict.upper_bound(word); ++pos) { cout << " " << pos->second << endl; } //print all keys for value "raffiniert" word = ("raffiniert"); cout << word << ": " << endl; for (pos = dict.begin(); pos != dict.end(); ++pos) { if (pos->second == word) { cout << " " << pos->first << endl; } } }
The program has the following output:
english german
--------------------
car Auto
clever raffiniert
day Tag
smart elegant
smart raffiniert
smart klug
strange fremd
strange seltsam
trait Merkmal
smart:
elegant
raffiniert
klug
raffiniert:
clever
smart
The following example shows how to use the global find_if() algorithm to find an element with a certain value:
// cont/mapfind.cpp #include <iostream> #include <algorithm> #include <map> using namespace std; /*function object to check the value of a map element */ template <class K, class V> class value_equals { private: V value; public: //constructor (initialize value to compare with) value_equals (const V& v) : value(v) { } //comparison bool operator() (pair<const K, V> elem) { return elem.second == value; } }; int main() { typedef map<float,float> FloatFloatMap; FloatFloatMap coll; FloatFloatMap::iterator pos; //fill container coll[1]=7; coll[2]=4; coll[3]=2; coll[4]=3; coll[5]=6; coll[6]=1; coll[7]=3; //search an element with key 3.0 pos = coll.find (3.0); // logarithmic complexity if (pos != coll.end()) { cout << pos->first << ": " << pos->second << endl; } //search an element with value 3.0 pos = find_if (coll.begin(),coll.end(), // linear complexity value_equals<float,float>(3.0)); if (pos != coll.end()) { cout << pos->first << ": " << pos->second << endl; } }
The output of the program is as follows:
3: 2 4: 3
Here is another example. It is for advanced programmers rather than STL beginners. You can take it as an example of both the power and the snags of the STL. In particular, this example demonstrates the following techniques:
How to use maps
How to write and use function objects
How to define a sorting criterion at runtime
How to compare strings in a case-insensitive way
// cont/mapcmp.cpp #include <iostream> #include <iomanip> #include <map> #include <string> #include <algorithm> using namespace std; /*function object to compare strings *-allows you to set the comparison criterion at runtime *-allows you to compare case insensitive */ class RuntimeStringCmp { public: //constants for the comparison criterion enum cmp_mode {normal, nocase}; private: //actual comparison mode const cmp_mode mode; //auxiliary function to compare case insensitive static bool nocase_compare (char c1, char c2) { return toupper(c1) < toupper(c2); } public: //constructor: initializes the comparison criterion RuntimeStringCmp (cmp_mode m=normal) : mode(m) { } //the comparison bool operator() (const string& s1, const string& s2) const { if (mode == normal) { return s1<s2; } else { return lexicographical_compare (s1.begin(), s1.end(), s2.begin(), s2.end(), nocase_compare); } } }; /*container type: *-map with * -string keys * -string values * -the special comparison object type */ typedef map<string,string,RuntimeStringCmp> StringStringMap; //function that fills and prints such containers void fillAndPrint(StringStringMap& coll); int main() { //create a container with the default comparison criterion StringStringMap coll1; fillAndPrint(coll1); //create an object for case-insensitive comparisons RuntimeStringCmp ignorecase (RuntimeStringCmp::nocase); //create a container with the case-insensitive comparisons criterion StringStringMap coll2 (ignorecase); fillAndPrint (coll2); } void fillAndPrint (StringStringMap& coll) { //fill insert elements in random order coll["Deutschland"] = "Germany"; coll["deutsch"] = "German"; coll["Haken"] = "snag"; coll["arbeiten"] = "work"; coll["Hund"] = "dog"; coll["gehen"] = "go"; coll["Unternehmen"] = "enterprise"; coll["unternehmen"] = "undertake"; coll["gehen"] = "walk"; coll["Bestatter"] = "undertaker"; //print elements StringStringMap::iterator pos; cout.setf(ios::left, ios::adjustfield); for (pos=coll.begin(); pos!=coll.end(); ++pos) { cout << setw(15) << pos->first.c_str() << " " << pos->second << endl; } cout << endl; }
main() creates two containers and calls fillAndPrint() for them. fillAndPrint() fills the containers with the same elements and prints the contents of them. However, the containers have two different sorting criteria:
coll1 uses the default function object of type RuntimeStringCmp, which compares the elements by using operator <.
coll2 uses a function object of type RuntimeStringCmp that is initialized by value nocase of class RuntimeStringCmp. nocase forces this function object to sort strings in a case-insensitive way.
The program has the following output:
Bestatter undertaker Deutschland Germany Haken snag Hund dog Unternehmen enterprise arbeiten work deutsch German gehen walk unternehmen undertake arbeiten work Bestatter undertaker deutsch German Deutschland Germany gehen walk Haken snag Hund dog Unternehmen undertake
The first block of the output prints the contents of the first container that compares with operator <. The output starts with all uppercase keys followed by all lowercase keys.
The second block prints all case-insensitive items, so the order changed. But note, the second block has one item less. This is because the uppercase word "Unternehmen" is, from a case-insensitive point of view, equal to the lowercase word "unternehmen,"[29] and we use a map that does not allow duplicates according to its comparison criterion. Unfortunately the result is a mess because the German key that is the translation for "enterprise" got the value "undertake." So probably a multimap should be used here. This makes sense because a multimap is the typical container for dictionaries.
The STL is a framework. In addition to the standard container classes it allows you to use other data structures as containers. You can use strings or ordinary arrays as STL containers, or you can write and use special containers that meet special needs. Doing this has the advantage that you can benefit from algorithms, such as sorting or merging, for your own type. Such a framework is a good example of the Open Closed Principle[30]: open for extension; closed for modification.
There are three different approaches to making containers "STL-able":
The invasive approach[31]
You simply provide the interface that ah STL container requires. In particular, you need the usual member functions of containers such as begin() and end(). This approach is invasive because it requires that a container be written in a certain way.
The noninvasive approach[31]
You write or provide special iterators that are used as an interface between the algorithms and special containers. This approach is noninvasive. All it requires is the ability to step through all of the elements of a container, an ability that any container provides in some way.
The wrapper approach
Combining the two previous approaches, you write a wrapper class that encapsulates any data structure with an STL container-like interface.
This subsection first discusses strings as a standard container, which is an example of the invasive approach. It then covers an important standard container that uses the noninvasive approach: ordinary arrays. However, you can also use the wrapper approach to access data of an ordinary array. Finally, this section subdiscusses some aspects of an important container that is not part of the standard: a hash table.
Whoever wants to write an STL container might also support the ability to get parameterized for different allocators. The C++ standard library provides some special functions and classes for programming with allocators and uninitialized memory. See Section 15.2, for details.
The string classes of the C++ standard library are an example of the invasive approach of writing STL containers (string classes are introduced and discussed in Chapter 11). Strings can be considered containers of characters. The characters inside the string build a sequence over which you can iterate to process the individual characters. Thus, the standard string classes provide the container interface of the STL. They provide the begin() and end() member functions, which return random access iterators to iterate over a string. They also provide some operations for iterators and iterator adapters. For example, push_back() is provided to enable the use of back inserters.
Note that string processing from the STL's point of view is a bit unusual. This is because normally you process strings as a whole object (you pass, copy, or assign strings). However, when individual character processing is of interest, the ability to use STL algorithms might be helpful. For example, you could read the characters with istream iterators or you could transform string characters, such as make them uppercase or lowercase. In addition, by using STL algorithms you can use a special comparison criterion for strings. The standard string interface does not provide that ability.
Section 11.2.13, which is part of the string chapter, discusses the STL aspects of strings in more detail and gives examples.
You can use ordinary arrays as STL containers. However, ordinary arrays are not classes, so they don't provide member functions such as begin() and end(), and you can't define member functions for them. Here, either the noninvasive approach or the wrapper approach must be used.
Using the noninvasive approach is simple. You only need objects that are able to iterate over the elements of an array by using the STL iterator interface. Actually, such iterators already exist: ordinary pointers. It was a design decision of the STL to use the pointer interface for iterators so that you could use ordinary pointers as iterators. This again shows the generic concept of pure abstraction: Anything that behaves like an iterator is an iterator. In fact, pointers are random access iterators (see Section 7.2.5,). The following example demonstrates how to use ordinary arrays as STL containers:
// cont/array1.cpp #include <iostream> #include <algorithm> #include <functional> using namespace std; int main() { int coll[] = { 5, 6, 2, 4, 1, 3 }; //square all elements transform (coll, coll+6, // first source coll, // second source coll, // destination multiplies<int>()); // operation //sort beginning with the second element sort (coll+1, coll+6); //print all elements copy (coll, coll+6, ostream_iterator<int>(cout," ")); cout << endl; }
You must be careful to pass the correct end of the array, as it is done here by using coll+6. And, as usual, you have to make sure that the end of the range is the position after the last element.
The output of the program is as follows:
25 1 4 9 16 36
Additional examples are on page 382 and page 421.
In his book The C++ Programming Language, 3rd edition, Bjarne Stroustrup introduces a useful wrapper class for ordinary arrays. It is safer and has no worse performance than an ordinary array. It also is a good example of a user-defined STL container. This container uses the wrapper approach because it offers the usual container interface as a wrapper around the array.
The class carray (the name is short for "C array" or for "constant size array") is defined as follows[32]:
// cont/carray.hpp #include <cstddef> template<class T, size_t thesize> class carray { private: T v[thesize]; // fixed-size array of elements of type T public: //type definitions typedef T value_type; typedef T* iterator; typedef const T* const_iterator; typedef T& reference; typedef const T& const_reference; typedef size_t size_type; typedef ptrdiff_t difference_type; //iterator support iterator begin() { return v; } const_iterator begin() const { return v; } iterator end() { return v+thesize; } const_iterator end() const { return v+thesize; } //direct element access reference operator[](size_t i) { return v[i]; } const_reference operator[](size_t i) const { return v[i]; } //size is constant size_type size() const { return thesize; } size_type max_size() const { return thesize; } //conversion to ordinary array T* as_array() { return v; } };
Here is an example of the usage of the carray class:
// cont/carray1.cpp #include <algorithm> #include <functional> #include "carray.hpp" #include "print.hpp" using namespace std; int main() { carray<int,10> a; for (unsigned i=0; i<a.size(); ++i) { a[i] = i+1; } PRINT_ELEMENTS(a); reverse(a.begin(),a.end()); PRINT_ELEMENTS(a); transform (a. begin(),a.end(), // source a. begin(), // destination negate<int>()); // operation PRINT_ELEMENTS(a); }
As you can see, you can use the general container interface operations (begin(), end(), and operator [ ]) to manipulate the container directly. Therefore, you can also use different operations that call begin() and end(), such as algorithms and the auxiliary function PRINT_ELEMENTS(), which is introduced on page 118.
The output of the program is as follows:
1 2 3 4 5 6 7 8 9 10 10 9 8 7 6 5 4 3 2 1 -10 -9 -8 -7 -6 -5 -4 -3 -2 -1
One important data structure for collections is not part of the C++ standard library: the hash table. There were suggestions to incorporate hash tables into the standard; however, they were not part of the original STL and the committee decided that the proposal for their inclusion came too late. (At some point you have to stop introducing features and focus on the details. Otherwise, you never finish the work.)
Nevertheless, inside the C++ community several implementations of hash tables are available. Libraries typically provide four kinds of hash tables: hash_set, hash_multiset, hash_map, and hash_multimap. According to the other associative containers, the multi versions allow duplicates and maps contain key/value pairs. Bjarne Stroustrup discusses hash_map as an example of a supplemented STL container in detail in Section 17.6 of his book The C+ + Programming Language, 3rd edition. For a concrete implementation of hash containers, see, for example, the "STLport" (http://www.stlport.org/). Note that different implementations may differ in details because hash containers are not yet standardized.
In general, STL container classes provide value semantics and not reference semantics. Thus, they create internal copies of the elements they contain and return copies of those elements. Section 5.10.2, discusses the pros and cons of this approach and touches on its consequences. To summarize, if you want reference semantics in STL containers (whether because copying elements is expensive or because identical elements will be shared by different collections), you should use a smart pointer class that avoids possible errors. Here is one possible solution to the problem. It uses an auxiliary smart pointer class that enables reference counting for the objects to which the pointers refer[33]:
// cont/countptr.hpp #ifndef COUNTED_PTR_HPP #define COUNTED_PTR_HPP /*class for counted reference semantics *-deletes the object to which it refers when the last CountedPtr * that refers to it is destroyed */ template <class T> class CountedPtr { private: T* ptr; // pointer to the value long* count; // shared number of owners public: //initialize pointer with existing pointer //-requires that the pointer p is a return value of new explicit CountedPtr (T* p=0) : ptr(p), count(new long(1)) { } //copy pointer (one more owner) CountedPtr (const CountedPtr<T>& p) throw() : ptr(p.ptr), count(p.count) { ++*count; } //destructor (delete value if this was the last owner) ~CountedPtr () throw() { dispose(); } //assignment (unshare old and share new value) CountedPtr<T>& operator= (const CountedPtr<T>& p) throw() { if (this != &p) { dispose(); ptr = p.ptr; count = p.count; ++*count; } return *this; } //access the value to which the pointer refers T& operator*() const throw() { return *ptr; } T* operator->() const throw() { return ptr; } private: void dispose() { if (--*count == 0) { delete count; delete ptr; } } }; #endif /*COUNTED_PTR_HPP*/
This class resembles the standard auto_ptr class (see Section 4.2,). It expects that the values with which the smart pointers are initialized are return values of operator new. However, unlike auto_ptr, it allows you to copy these smart pointers while retaining the validity of the original and the copy. Only if the last smart pointer to the object gets destroyed does the value to which it refers get deleted.
You could improve the class to allow automatic type conversions or the ability to transfer the ownership away from the smart pointers to the caller.
The following program demonstrates how to use this class:
// cont/refsem1.cpp #include <iostream> #include <list> #include <deque> #include <algorithm> #include "countptr.hpp" using namespace std; void printCountedPtr (CountedPtr<int> elem) { cout << *elem << ' '; } int main() { //array of integers (to share in different containers) static int values[] ={3, 5, 9, 1,6,4}; //two different collections typedef CountedPtr<int> IntPtr; deque<IntPtr> coll1; list<IntPtr> coll2; /*insert shared objects into the collections *-same order in coll1 *-reverse order in coll2 */ for (int i=0; i<sizeof(values)/sizeof(values[0] ); ++i) { IntPtr ptr(new int(values[i])); coll1.push_back(ptr); coll2.push_front(ptr); } //print contents of both collections for_each (coll1.begin(), coll1.end(), printCountedPtr); cout << endl; for_each (coll2.begin(), coll2.end(), printCountedPtr); cout << endl << endl; /*modify values at different places *-square third value in coll1 *-negate first value in coll1 *-set first value in coll2 to 0 */ *coll1[2] *= *coll1[2]; (**coll1.begin()) *= -1; (**coll2.begin()) = 0; //print contents of both collections again for_each (coll1.begin(), coll1.end(), printCountedPtr); cout << endl; for_each (coll2.begin(), coll2.end(), printCountedPtr); cout << endl; }
The program has the following output:
3 5 9 1 6 4 4 6 1 9 5 3 -3 5 81 1 6 0 0 6 1 81 5 -3
Note that if you call an auxiliary function that saves one element of the collections (an IntPtr) somewhere else, the value to which it refers stays valid even if the collections get destroyed or all of their elements are removed.
See the Boost repository for C++ libraries at http://www.boost.org/ for a collection of different smart pointer classes as an extension of the C++ standard library. (Class CountedPtr<> will probably be called shared_ptr<>.)
The C++ standard library provides different container types with different abilities. The question now is: When do you use which container type? Table 6.9 provides an overview. However, it contains general statements that might not fit in reality. For example, if you manage only a few elements you can ignore the complexity because short element processing with linear complexity is better than long element processing with logarithmic complexity.
As a supplement to the table, the following rules of thumb might help:
By default, you should use a vector. It has the simplest internal data structure and provides random access. Thus, data access is convenient and flexible, and data processing is often fast enough.
If you insert and/or remove elements often at the beginning and the end of a sequence, you should use a deque. You should also use a deque if it is important that the amount of internal memory used by the container shrinks when elements are removed. Also, because a vector usually uses one block of memory for its elements, a deque might be able to contain more elements because it uses several blocks.
If you insert, remove, and move elements often in the middle of a container, consider using a list. Lists provide special member functions to move elements from one container to another in constant time. Note, however, that because a list provides no random access, you might suffer significant performance penalties on access to elements inside the list if you only have the beginning of the list.
Like all node-based containers, a list doesn't invalidate iterators that refer to elements, as long as those elements are part of the container. Vectors invalidate all of their iterators, pointers, and references whenever they exceed their capacity, and part of their iterators, pointers, and references on insertions and deletions. Deques invalidate iterators, pointers, and references when they change their size, respectively.
If you need a container that handles exceptions in a way that each operation either succeeds or has no effect, you should use either a list (without calling assignment operations and sort() and, if comparing the elements may throw, without calling merge (), remove(), remove_if(), and unique(); see page 172) or an associative container (without calling the multiple-element insert operations and, if copying/assigning the comparison criterion may throw, without calling swap()). See Section 5.11.2, for a general discussion of exception handling in the STL and Section 6.10.10, for a table of all container operations with special guarantees in face of exceptions.
If you often need to search for elements according to a certain criterion, use a set or a multiset that sorts elements according to this sorting criterion. Keep in mind that the logarithmic complexity involved in sorting 1,000 elements is in principle ten times better than that with linear complexity. In this case, the typical advantages of binary trees apply.
A hash table commonly provides five to ten times faster lookup than a binary tree. So if a hash container is available, you might consider using it even though hash tables are not standardized. However, hash containers have no ordering, so if you need to rely on element order they're no good. Because they are not part of the C++ standard library, you should have the source code to stay portable.
To process key/value pairs, use a map or a multimap (or the hash version, if available).
If you need an associative array, use a map.
If you need a dictionary, use a multimap.
| Vector | Deque | List | Set | Multiset | Map | Multimap | |
| Typical internal data structure | Dynamic array | Array of arrays | Doubly linked list | Binary tree | Binary tree | Binary tree | Binary tree |
| Elements | Value | Value | Value | Value | Value | Key/value pair | Key/value pair |
| Duplicates allowed | Yes | Yes | Yes | No | Yes | Not for the key | Yes |
| Random access available | Yes | Yes | No | No | No | With key | No |
| Iterator category | Random access | Random access | Bidirectional | Bidirectional (element constant) | Bidirectional (element constant) | Bidirectional (key constant) | Bidirectional (key constant) |
| Search/find elements | Slow | Slow | Very slow | Fast | Fast | Fast for key | Fast for key |
| Inserting/removing of elements is fast | At the end | At the beginning and the end | Anywhere | — | — | — | — |
| Inserting/removing invalidates iterators, references, pointers | On reallocation | Always | Never | Never | Never | Never | Never |
| Frees memory for removed elements | Never | Sometimes | Always | Always | Always | Always | Always |
| Allows memory reservation | Yes | No | — | — | — | — | — |
| Transaction safe (success or no effect) | Push/pop at the end | Push/pop at the beginning and the end | All except sort() and assignments | All except multiple-element insertions | All except multiple-element insertions | All except multiple-element insertions | All except multiple-element insertions |
A problem that is not easy to solve is how to sort objects according to two different sorting criteria. For example, you might have to keep elements in an order provided by the user while providing search capabilities according to another criterion. And as in databases, you need fast access regarding two or more different criteria. In this case, you could probably use two sets or two maps that share the same objects with different sorting criteria. However, having objects in two collections is a special issue, which is covered in Section 6.8.
The automatic sorting of associative containers does not mean that these containers perform better when sorting is needed. This is because an associative container sorts each time a new element gets inserted. An often faster way is to use a sequence container and to sort all elements after they are all inserted by using one of the several sort algorithms (see Section 9.2.2).
The following are two simple programs that sort all strings read from the standard input and print them without duplicates by using two different containers:
Using a set:
// cont/sortset.cpp #include <iostream> #include <string> #include <algorithm> #include <set> using namespace std; int main() { /*create a string set *-initialized by all words from standard input */ set<string> coll((istream_iterator<string>(cin)),(istream_iterator<string>())); //print all elements copy (coll.begin(), coll.end(), ostream_iterator<string>(cout, "\n")); }
Using a vector:
// cont/sortvec.cpp #include <iostream> #include <string> #include <algorithm> #include <vector> using namespace std; int main() { /*create a string vector *-initialized by all words from standard input */ vector<string> coll((istream_iterator<string>(cin)), (istream_iterator<string>())); //sort elements sort (coll.begin(), coll.end()); //print all elements ignoring subsequent duplicates unique_copy (coll.begin(), coll.end(), ostream_iterator<string>(cout, "\n")); }
When I tried both programs with about 150,000 strings on my system, the vector version was approximately 10% faster. Inserting a call of reserve() made the vector version 5% faster. Allowing duplicates (using a multiset instead of a set and calling copy() instead of unique_copy() respectively) changed things dramatically: The vector version was more than 40% faster! These measurements are not representative; however, they do show that it is often worth trying different ways of processing elements.
In practice, predicting which container type is the best is often difficult. The big advantage of the STL is that you can try different versions without much effort. The major work— implementing the different data structures and algorithms— is done. You have only to combine them in a way that is best for you.
This section discusses the different STL containers and presents all of the operations that STL containers provide. The types and members are grouped by functionality. For each type and operation this section describes the signature, the behavior, and the container types that provide it. Possible containers are vector, deques, lists, sets, multisets, maps, multimaps, and strings. In the following subsections, container means the container type that provides the member.
container::value_type
The type of elements.
For sets and multisets, it is constant.
For maps and multimaps, it is pair <const key-type, value-type>
Provided by vectors, deques, lists, sets, multisets, maps, multimaps, and strings.
container::reference
The type of element references.
Typically: container::value_type&.
For vector<bool>, it is an auxiliary class (see page 158).
Provided by vectors, deques, lists, sets, multisets, maps, multimaps, and strings.
container::const_reference
The type of constant element references.
Typically: const container::value_type&.
For vector<bool>, it is bool.
Provided by vectors, deques, lists, sets, multisets, maps, multimaps, and strings.
container::iterator
The type of iterators.
Provided by vectors, deques, lists, sets, multisets, maps, multimaps, and strings.
container::const_iterator
The type of constant iterators.
Provided by vectors, deques, lists, sets, multisets, maps, multimaps, and strings.
container::reverse_iterator
The type of reverse iterators.
Provided by vectors, deques, lists, sets, multisets, maps, and multimaps.
container::const_reverse_iterator
The type of constant reverse iterators.
Provided by vectors, deques, lists, sets, multisets, maps, multimaps, and strings.
container::size_type
The unsigned integral type for size values.
Provided by vectors, deques, lists, sets, multisets, maps, multimaps, and strings.
container::difference_type
The signed integral type for difference values.
Provided by vectors, deques, lists, sets, multisets, maps, multimaps, and strings.
container::key_type
The type of the key of the elements for associative containers.
For sets and multisets, it is equivalent to value_type.
Provided by sets, multisets, maps, and multimaps.
container::mapped_type
The type of the value of the elements of associative containers.
Provided by maps and multimaps.
container::key_compare
The type of the comparison criterion of associative containers.
Provided by sets, multisets, maps, and multimaps.
container::value_compare
The type of the comparison criterion for the whole element type.
For sets and multisets, it is equivalent to key_compare.
For maps and multimaps, it is an auxiliary class for a comparison criterion that compares only the key part of two elements.
Provided by sets, multisets, maps, and multimaps.
container::allocator_type
The type of the allocator.
Provided by vectors, deques, lists, sets, multisets, maps, multimaps, and strings.
Containers provide the following constructors and destructors. Also, most constructors allow you to pass an allocator as an additional argument (see Section 6.10.9).
container::container ()
The default constructor.
Creates a new empty container.
Provided by vectors, deques, lists, sets, multisets, maps, multimaps, and strings.
explicit container::container (const CompFunc& op)
Creates a new empty container with op used as the sorting criterion (see page 191 and page 213 for examples).
The sorting criterion must define a "strict weak ordering" (see page 176).
Provided by sets, multisets, maps, and multimaps.
explicit container::container (const container&, c)
The copy constructor.
Creates a new container as a copy of the existing container c.
Calls the copy constructor for every element in c.
Provided by vectors, deques, lists, sets, multisets, maps, multimaps, and strings.
explicit container::container (size_type num)
Creates a container with num elements.
The elements are created with their default constructor.
Provided by vectors, deques, and lists.
container::container (size_type num, const T& value)
Creates a container with num elements.
The elements are created as copies of value.
T is the type of the container elements.
For strings, value is not passed by reference.
Provided by vectors, deques, lists, and strings.
container::container (InputIterator beg, InputIterator end)
Creates a container that is initialized by all elements of the range [beg,end).
This function is a member template (see page 11). Thus, the elements of the source range may have any type that is convertible to the element type of the container.
Provided by vectors, deques, lists, sets, multisets, maps, multimaps, and strings.
container::container (InputIterator beg, InputIterator end, const CompFunc& op)
Creates a container that has the sorting criterion op and is initialized by all elements of the range [beg,end).
This function is a member template (see page 11). Thus, the elements of the source range may have any type that is convertible to the element type of the container.
The sorting criterion must define a "strict weak ordering" (see page 176).
Provided by sets, multisets, maps, and multimaps.
container::~container ()
The destructor.
Removes all elements and frees the memory.
Calls the destructor for every element.
Provided by vectors, deques, lists, sets, multisets, maps, multimaps, and strings.
size_type container::size () const
Returns the actual number of elements.
To check whether the container is empty (contains no elements), you should use empty() because it may be faster.
Provided by vectors, deques, lists, sets, multisets, maps, multimaps, and strings.
bool container::empty () const
Returns whether the container is empty (contains no elements).
It is equivalent to container:: size()==0, but it may be faster (especially for lists).
Provided by vectors, deques, lists, sets, multisets, maps, multimaps, and strings.
size_type container::max_size () const
Returns the maximum number of elements a container may contain.
This is a technical value that may depend on the memory model of the container. In particular, because vectors usually use one memory segment, this value may be less than for other containers.
Provided by vectors, deques, lists, sets, multisets, maps, multimaps, and strings.
size_type container::capacity () const
Returns the number of elements the container may contain without reallocation.
Provided by vectors and strings.
void container::reserve (size_type num)
Reserves internal memory for at least num elements.
If num is less than the actual capacity, this call has no effect on vectors and is a nonbinding shrink request for strings.
To shrink the capacity of vectors, see the example on page 149.
Each reallocation invalidates all references, pointers, and iterators, and takes some time. Thus reserve() can increase speed and keep references, pointers, and iterators valid (see page 149 for details).
Provided by vectors and strings.
bool comparison (const container& c1, const container&, c2)
Returns the result of the comparison of two containers of same type.
comparison might be any of the following:
operator == operator != operator < operator > operator <= operator >=
Two containers are equal if they have the same number of elements and contain the same elements in the same order (all comparisons of two corresponding elements have to yield true).
To check whether a container is less than another container, the containers are compared lexicographically. See the description of the lexicographical_compare() algorithm on page 360 for a description of lexicographical comparison.
Provided by vectors, deques, lists, sets, multisets, maps, multimaps, and strings.
The member functions mentioned here are special implementations of corresponding STL algorithms that are discussed in Section 9.5 and Section 9.9. They provide better performance because they rely on the fact that the elements of associative containers are sorted. In fact, they provide logarithmic complexity instead of linear complexity. For example, to search for one of 1,000 elements, no more than ten comparisons on average are needed (see Section 2.3).
size_type container::count (const T& value) const
Returns the number of elements that are equal to value.
This is the special version of the count() algorithm discussed on page 338.
T is the type of the sorted value:
For sets and multisets, it is the type of the elements.
For maps and multimaps, it is the type of the keys.
Complexity: linear.
Provided by sets, multisets, maps, and multimaps.
iterator container::find (const T& value)
const_iterator container::find (const T& value) const
Both return the position of the first element that has a value equal to value.
They return end() if no element is found.
These are the special versions of the find() algorithm discussed on page 341.
T is the type of the sorted value:
For sets and multisets, it is the type of the elements.
For maps and multimaps, it is the type of the keys.
Complexity: logarithmic.
Provided by sets, multisets, maps, and multimaps.
iterator container::lower_bound (const T& value)
const_iterator container::lower_bound (const T& value) const
Both return the first position where a copy of value would get inserted according to the sorting criterion.
They return end() if no such element is found.
The return value is the position of the first element that has a value less than or equal to value (which might be end()).
These are the special versions of the lower_bound() algorithm discussed on page 413.
T is the type of the sorted value:
For sets and multisets, it is the type of the elements.
For maps and multimaps, it is the type of the keys.
Complexity: logarithmic.
Provided by sets, multisets, maps, and multimaps.
iterator container::upper_bound (const T& value)
const_iterator container::upper_bound (const T& value) const
Both return the last position where a copy of value would get inserted according to the sorting criterion.
They return end() if no such element is found.
The return value is the position of the first element that has a value greater than value (which might be end()).
These are the special versions of the upper_bound() algorithm discussed on page 413.
T is the type of the sorted value:
For sets and multisets, it is the type of the elements.
For maps and multimaps, it is the type of the keys.
Complexity: logarithmic.
Provided by sets, multisets, maps, and multimaps.
pair<iterator,iterator> container::equal_range (const T& value)
pair<const_iterator,const_iterator> container::equal_range (const T& value) const
Both return a pair with the first and last positions where a copy of value would get inserted according to the sorting criterion.
The return value is the range of elements equal to value.
They are equivalent to:
make_pair (lower_bound(value),upper_bound(value))
These are the special versions of the equal_range() algorithm discussed on page 415.
T is the type of the sorted value:
For sets and multisets, it is the type of the elements.
For maps and multimaps, it is the type of the keys.
Complexity: logarithmic.
Provided by sets, multisets, maps, and multimaps.
key_compare container::key_comp ()
Returns the comparison criterion.
Provided by sets, multisets, maps, and multimaps.
value_compare container::value_comp ()
Returns the object that is used as the comparison criterion.
For sets and multisets, it is equivalent to key_comp ().
For maps and multimaps, it is an auxiliary class for a comparison criterion that compares only the key part of two elements.
Provided by sets, multisets, maps, and multimaps.
container& container::operator= (const container& c)
Assigns all elements of c; that is, it replaces all existing elements with copies of the elements of c.
The operator may call the assignment operator for elements that have been overwritten, the copy constructor for appended elements, and the destructor of the element type for removed elements.
Provided by vectors, deques, lists, sets, multisets, maps, multimaps, and strings.
void container::assign (size_type num, const T& value)
Assigns num occurrences of value; that is, it replaces all existing elements by num copies of value.
T has to be the element type.
Provided by vectors, deques, lists, and strings.
void container::assign (InputIterator beg, Inputlterator end)
Assigns all elements of the range [beg,end); that is, it replaces all existing elements with copies of the elements of [beg,end).
This function is a member template (see page 11). Thus, the elements of the source range may have any type that is convertible to the element type of the container.
Provided by vectors, deques, lists, and strings.
void container::swap (container& c)
Swaps the contents with c.
Both containers swap
their elements and
their sorting criterion if any.
This function has a constant complexity. You should always prefer it over an assignment when you no longer need the assigned object (see Section 6.1.2).
For associative containers, the function may only throw if copying or assigning the comparison criterion may throw. For all other containers, the function does not throw.
Provided by vectors, deques, lists, sets, multisets, maps, multimaps, and strings.
void swap (container& c1, container&, c2)
It is equivalent to c1. swap(c2) (see the previous description).
For associative containers, the function may only throw if copying or assigning the comparison criterion may throw. For all other containers, the function does not throw.
Provided by vectors, deques, lists, sets, multisets, maps, multimaps, and strings.
reference container::at (size_type idx)
const_reference container::at (size_type idx) const
Both return the element with the index idx (the first element has index 0).
Passing an invalid index (less than 0 or equal to size() or greater than size()) throws an out_of _range exception.
Note that the returned reference may get invalidated due to later modifications or reallocations.
If you are sure that the index is valid, you can use operator [ ], which is faster.
Provided by vectors, deques, and strings.
reference container::operator [ ] (size_type idx)
const_reference container::operator [ ] (size_type idx) const
Both return the element with the index idx (the first element has index 0).
Passing an invalid index (less than 0 or equal to size() or greater than size()) results in undefined behavior. Thus, the caller must ensure that the index is valid; otherwise, at() should be used.
The reference returned for the nonconstant string may get invalidated due to string modifications or reallocations (see page 487 for details).
Provided by vectors, deques, and strings.
T& map::operator [] (const key_type& key)
Operator [ ] for associative arrays.
Returns the corresponding value to key in a map.
Note: If no element with a key equal to key exists, this operation creates a new element automatically with a value that is initialized by the default constructor of the value type. Thus, you can't have an invalid index (only wrong behavior). For example:
map<int,string> coll;
coll [77] = "hello"; // insert key 77 with value "hello"
cout << coll [42]; // Oops, inserts key 42 with value "" and prints the value
See Section 6.6.3, for details.
T is the type of the element value.
It is equivalent to:
(*((insert(make_pair(x,T()))).first)).second
Provided by maps.
reference container::front ()
const_reference container::front () const
Both return the first element (the element with index 0).
The caller must ensure that the container contains an element (size ()>0); otherwise, the behavior is undefined.
Provided by vectors, deques, and lists.
reference container::back ()
const_reference container::back () const
Both return the last element (the element with index size()-l).
The caller must ensure that the container contains an element (size()>0); otherwise, the behavior is undefined.
Provided by vectors, deques, and lists.
The following member functions return iterators to iterate over the elements of the containers. Table 6.34 lists the iterator category (see Section 7.2,) according to the different container types.
| Container | Iterator Category |
|---|---|
| Vector | Random access |
| Deque | Random access |
| List | Bidirectional |
| Set | Bidirectional, element is constant |
| Multiset | Bidirectional, element is constant |
| Map | Bidirectional, key is constant |
| Multimap | Bidirectional, key is constant |
| String | Random access |
iterator container::begin ()
const_iterator container:: begin () const
Both return an iterator for the beginning of the container (the position of the first element).
If the container is empty, the calls are equivalent to container::end().
Provided by vectors, deques, lists, sets, multisets, maps, multimaps, and strings.
iterator container::end ()
const_iterator container::end () const
Both return an iterator for the end of the container (the position after the last element).
If the container is empty, the calls are equivalent to container: : begin().
Provided by vectors, deques, lists, sets, multisets, maps, multimaps, and strings.
reverse_iterator container::rbegin ()
const_reverse_iterator container::rbegin () const
Both return a reverse iterator for the beginning of a reverse iteration over the elements of the container (the position of the last element).
If the container is empty, the calls are equivalent to container:: rend().
For details about reverse iterators, see Section 7.4.1.
Provided by vectors, deques, lists, sets, multisets, maps, multimaps, and strings.
reverse_iterator container::rend ()
const_reverse_iterator container::rend () const
Both return a reverse iterator for the end of a reverse iteration over the elements of the container (the position before the first element).
If the container is empty, the calls are equivalent to container:: rbegin().
For details about reverse iterators, see Section 7.4.1.
Provided by vectors, deques, lists, sets, multisets, maps, multimaps, and strings.
iterator container::insert (const T& value)
pair<iterator,bool> container::insert (const T& value)
Both insert a copy of value into an associative container.
Containers that allow duplicates (multisets and multimaps) have the first signature. They return the position of the new element.
Containers that do not allow duplicates (sets and maps) have the second signature. If they can't insert the value because an element with an equal value or key exists, they return the position of the existing element and false. If they can insert the value, they return the position of the new element and true.
T is the type of the container elements. Thus, for maps and multimaps it is a key/value pair.
The functions either succeed or have no effect.
Provided by sets, multisets, maps, and multimaps.
iterator container::insert (iterator pos, const T& value)
Inserts a copy of value at the position of iterator pos.
Returns the position of the new element.
For associative containers (sets, multisets, maps, and multimaps), the position is only used as hint, pointing to where the insert should start to search. If value is inserted right behind pos the function has amortized constant complexity; otherwise, it has logarithmic complexity.
If the container is a set or a map that already contains an element equal to (the key of) value, then the call has no effect and the return value is the position of the existing element.
For vectors and deques, this operation might invalidate iterators and references to other elements.
T is the type of the container elements. Thus, for maps and multimaps it is a key/value pair.
For strings, value is not passed by reference.
For vectors and deques, if the copy operations (copy constructor and assignment operator) of the elements don't throw, the function either succeeds or has no effect. For all other standard containers, the function either succeeds or has no effect.
Provided by vectors, deques, lists, sets, multisets, maps, multimaps, and strings.
void container::insert (iterator pos, size_type num, const T& value)
Inserts num copies of value at the position of iterator pos.
For vectors and deques, this operation might invalidate iterators and references to other elements.
T is the type of the container elements. Thus, for maps and multimaps it is a key/value pair.
For strings, value is not passed by reference.
For vectors and deques, if the copy operations (copy constructor and assignment operator) of the elements don't throw, the function either succeeds or has no effect. For lists, the function either succeeds or has no effect.
Provided by vectors, deques, lists, and strings.
void container::insert (InputIterator beg, InputIterator end)
Inserts copies of all elements of the range [beg,end) into the associative container.
This function is a member template (see page 11). Thus, the elements of the source range may have any type that is convertible to the element type of the container.
Provided by sets, multisets, maps, and multimaps.
void container::insert (iterator pos, InputIterator beg, InputIterator end)
Inserts copies of all elements of the range [beg,end) at the position of iterator pos.
This function is a member template (see page 11). Thus, the elements of the source range may have any type that is convertible to the element type of the container.
For vectors and deques, this operation might invalidate iterators and references to other elements.
For lists, the function either succeeds or has no effect.
Provided by vectors, deques, lists, and strings.
void container::push_front (const T& value)
Inserts a copy of value as the new first element.
T is the type of the container elements.
It is equivalent to insert(begin(), value).
For deques, this operation invalidates iterators to other elements. References to other elements stay valid.
This function either succeeds or has no effect.
Provided by deques and lists.
void container::push_back (const T& value)
Appends a copy of value as the new last element.
T is the type of the container elements.
It is equivalent to insert(end() ,value).
For vectors, this operation invalidates iterators and references to other elements when reallocation takes place.
For deques, this operation invalidates iterators to other elements. References to other elements stay valid.
This function either succeeds or has no effect.
Provided by vectors, deques, lists, and strings.
void list::remove (const T& value)
void list::remove_if (UnaryPredicate op)
remove() removes all elements with value value.
remove_if() removes all elements for which the unary predicate
op(elem)
yields true.
Note that op should not change its state during a function call. See Section 8.1.4, for details.
Both call the destructors of the removed elements.
The order of the remaining arguments remains stable.
This is the special version of the remove() algorithm, which is discussed on page 378, for lists.
T is the type of the container elements.
For further details and examples, see page 170.
The functions may only throw if the comparison of the elements may throw.
Provided by lists.
size_type container::erase (const T& value)
Removes all elements equal to value from an associative container.
Returns the number of removed elements.
Calls the destructors of the removed elements.
T is the type of the sorted value:
For sets and multisets, it is the type of the elements.
For maps and multimaps, it is the type of the keys.
The function does not throw.
Provided by sets, multisets, maps, and multimaps.
void container::erase (iterator pos)
iterator container::erase (iterator pos)
Both remove the element at the position of iterator pos.
Sequence containers (vectors, deques, lists, and strings) have the second signature. They return the position of the following element (or end()).
Associative containers (sets, multisets, maps, and multimaps) have the first signature. They return nothing.
Both call the destructors of the removed elements.
Note that the caller must ensure that the iterator pos is valid. For example:
coll. erase (coll. end()); // ERRORundefined behavior
For vectors and deques, this operation might invalidate iterators and references to other elements.
For vectors and deques, the function may only throw if the copy constructor or assignment operator of the elements may throw. For all other containers, the function does not throw.
Provided by vectors, deques, lists, sets, multisets, maps, multimaps, and strings.
void container::erase (iterator beg, iterator end)
iterator container::erase (iterator beg, iterator end)
Both remove the elements of the range [beg,end).
Sequence containers (vectors, deques, lists, and strings) have the second signature. They return the position of the element that was behind the last removed element on entry (or end()).
Associative containers (sets, multisets, maps, and multimaps) have the first signature. They return nothing.
As always for ranges, all elements including beg but excluding end are removed.
Both call the destructors of the removed elements.
Note that the caller must ensure that beg and end define a valid range that is part of the container.
For vectors and deques, this operation might invalidate iterators and references to other elements.
For vectors and deques, the function may only throw if the copy constructor or the assignment operator of the elements may throw. For all other containers, the function does not throw.
Provided by vectors, deques, lists, sets, multisets, maps, multimaps, and strings.
void container::pop_front ()
Removes the first element of the container.
It is equivalent to container. erase (container.begin()).
Note: If the container is empty, the behavior is undefined. Thus, the caller must ensure that the container contains at least one element (size () >0).
The function does not throw.
Provided by deques and lists.
void container::pop_back ()
Removes the last element of the container.
It is equivalent to container.erase(--container.end()), provided this expression is valid, which might not be the case for vectors (see page 258).
Note: If the container is empty, the behavior is undefined. Thus, the caller must ensure that the container contains at least one element (size()>0).
The function does not throw.
Provided by vectors, deques, and lists.
void container::resize (size_type num)
void container::resize (size_type num, T value)
Both change the number of elements to num.
If size() is num on entry, they have no effect.
If num is greater than size() on entry, additional elements are created and appended to the end of the container. The first form creates the new elements by calling their default constructor; the second form creates the new elements as copies of value.
If num is less than size() on entry, elements are removed at the end to get the new size. In this case, they call the destructor of the removed elements.
For vectors and deques, these functions might invalidate iterators and references to other elements.
For vectors and deques, these functions either succeed or have no effect, provided the copy constructor or the assignment operator of the elements don't throw. For lists, the functions either succeed or have no effect.
Provided by vectors, deques, lists, and strings.
void container::clear ()
Removes all elements (makes the container empty).
Calls the destructors of the removed elements.
Invalidates all iterators and references to the container.
For vectors and deques, the function may only throw if the copy constructor or the assignment operator of the elements may throw. For all other containers, the function does not throw.
Provided by vectors, deques, lists, sets, multisets, maps, multimaps, and strings.
void list:: unique ()
void list::unique (BinaryPredicate op)
Both remove subsequent duplicates of list elements so that each element contains a different value than the following element.
The first form removes all elements for which the previous values are equal.
The second form removes all elements that follow an element e and for which the binary predicate
op(elem,e)
yields true.[34] In other words, the predicate is not used to compare an element with its predecessor; the element is compared with the previous element that was not removed.
Note that op should not change its state during a function call. See Section 8.1.4, for details.
Both call the destructors of the removed elements.
These are the special versions of the unique() algorithms, which are discussed on page 381, for lists.
The functions do not throw if the comparisons of the elements do not throw.
void list::splice (iterator pos, list& source)
Moves all elements of source into *this and inserts them at the position of iterator pos.
source is empty after the call.
If source and *this are identical, the behavior is undefined. Thus, the caller must ensure that source is a different list. To move elements inside the same list you must use the following form of splice().
The caller must ensure that pos is a valid position of *this; otherwise, the behavior is undefined.
This function does not throw.
void list::splice (iterator pos, list& source, iterator sourcePos)
Moves the element at the position sourcePos of the list source into *this and inserts it at the position of iterator pos.
source and *this may be identical. In this case, the element is moved inside the list.
If source is a different list, it contains one element less after the operation.
The caller must ensure that pos is a valid position of *this, sourcePos is a valid iterator of source, and sourcePos is not source. end(); otherwise, the behavior is undefined.
This function does not throw.
void list::splice (iterator pos, list& source, iterator sourceBeg, iterator sourceEnd)
Moves the elements of the range [sourceBeg,sourceEnd) of the list source to *this and inserts it at the position of iterator pos.
source and *this may be identical. In this case, pos must not be part of the moved range, and the elements are moved inside the list.
If source is a different list, it contains less elements after the operation.
The caller must ensure that pos is a valid position of *this, and that sourceBeg and sourceEnd define a valid range that is part of source; otherwise, the behavior is undefined.
This function does not throw.
void list::sort ()
void list::sort (CompFunc op)
Both sort the elements in the list.
The first form sorts all elements in the list with operator <.
The second form sorts all elements in the list by calling op to compare two elements[35]:
op(elem1,elem2)
The order of elements that have an equal value remains stable (unless an exception is thrown).
These are the special versions of the sort() and stable_sort() algorithms, which are discussed on page 397.
void list::merge (list& source)
void list::merge (list& source, CompFunc op)
Both merge all elements of the list source into *this.
source is empty after the call.
If *this and source are sorted on entry according to the sorting criterion < or op, the resulting list is also sorted. Strictly speaking, the standard requires that both lists be sorted on entry. In practice, however, merging is also possible for unsorted lists. However, you should check this before you rely on it.
The first form uses operator < as the sorting criterion.
The second form uses op as the optional sorting criterion and is used to compare two elements[36]:
op (elem, sourceElem)
This is the special version of the merge() algorithm, which is discussed on page 416.
If the comparisons of the elements do not throw, the functions either succeed or have no effect.
void list::reverse ()
Reverses the order of the elements in a list.
This is the special version of the reverse() algorithm, which is discussed on page 386.
This function does not throw.
All STL containers can be used with a special memory model that is defined by an allocator object (see Chapter 15 for details). This subsection describes the members for allocator support.
Standard containers require that all instances of an allocator type are interchangeable. Thus, storage allocated from one container can be deallocated via another that has the same type. Therefore, it is no problem when elements (and their storage) are moved between containers of the same type.
container::allocator_type
The type of the allocator.
Provided by vectors, deques, lists, sets, multisets, maps, multimaps, and strings.
allocator_type container::get_allocator () const
Returns the memory model of the container.
Provided by vectors, deques, lists, sets, multisets, maps, multimaps, and strings.
explicit container container (const Allocator& alloc)
Creates a new empty container that uses the memory model alloc.
Provided by vectors, deques, lists, sets, multisets, maps, multimaps, and strings.
container::container (const CompFunc& op, const Allocator& alloc)
Creates a new empty container with op used as the sorting criterion that uses the memory model alloc.
The sorting criterion must define a "strict weak ordering" (see page 176).
Provided by sets, multisets, maps, and multimaps.
container::container (size.type num, const T& value, const Allocator& alloc)
Creates a container with num elements that uses the memory model alloc.
The elements are created as copies of value.
T is the type of the container elements. Note that for strings, value is passed by value.
Provided by vectors, deques, lists, and strings.
container::container (InputIterator beg, InputIterator end, const Allocator& alloc)
Creates a container that is initialized by all elements of the range [beg,end) and uses the memory model alloc.
This function is a member template (see page 11). Thus, the elements of the source range may have any type that is convertible to the element type of the container.
Provided by vectors, deques, lists, sets, multisets, maps, multimaps, and strings.
container::container (InputIterator beg, InputIterator end, const CompFunc& op, const Allocator& alloc)
Creates a container that has the sorting criterion op, is initialized by all elements of the range [beg,end), and uses the memory model alloc.
This function is a member template (see page 11). Thus, the elements of the source range may have any type that is convertible to the element type of the container.
The sorting criterion must define a "strict weak ordering" (see page 176).
Provided by sets, multisets, maps, and multimaps.
As mentioned in Section 5.11.2, containers provide different guarantees in the face of exceptions. In general, the C++ standard library will not leak resources or violate container invariants in the face of exceptions. However, some operations give stronger guarantees (provided the arguments meet some requirements): They may guarantee commit-or-rollback behavior, or they may even guarantee that they will never throw at all. Table 6.35 lists all operations that give these stronger guarantees.[37]
For vectors, deques, and lists, you also have guarantees for resize(). It is defined as having the effect of either calling erase() or calling insert() or doing nothing:
void container::resize (size_type num, T value = T())
{
if (num > size()) {
insert (end(), num-size(), value);
}
else if (num < size()) {
erase (begin()+num, end());
}
}
Thus, its guarantees are a combination of the guarantees of erase() and insert() (see page 244).
| Operation | Page | Guarantee |
|---|---|---|
| vector::push_back() | 241 | Either succeeds or has no effect |
| vector::insert() | 240 | Either succeeds or has no effect if copying/assigning elements doesn't throw |
| vector::pop_back() | 243 | Doesn't throw |
| vector::erase() | 242 | Doesn't throw if copying/assigning elements doesn't throw |
| vector::clear() | 244 | Doesn't throw if copying/assigning elements doesn't throw |
| vector::swap() | 237 | Doesn't throw |
| deque::push_back() | 241 | Either succeeds or has no effect |
| deque::push_front() | 241 | Either succeeds or has no effect |
| deque::insert() | 240 | Either succeeds or has no effect if copying/assigning elements doesn't throw |
| deque::pop_back() | 243 | Doesn't throw |
| deque::pop_front() | 243 | Doesn't throw |
| deque::erase() | 242 | Doesn't throw if copying/assigning elements doesn't throw |
| deque::clear() | 244 | Doesn't throw if copying/assigning elements doesn't throw |
| deque::swap() | 237 | Doesn't throw |
| list::push_back() | 241 | Either succeeds or has no effect |
| list::push_front() | 241 | Either succeeds or has no effect |
| list::insert() | 240 | Either succeeds or has no effect |
| list::pop_back() | 243 | Doesn't throw |
| list::pop_front() | 243 | Doesn't throw |
| list::erase() | 242 | Doesn't throw |
| list:: clear() | 244 | Doesn't throw |
| list:: remove() | 242 | Doesn't throw if comparing the elements doesn't throw |
| list::remove_if() | 242 | Doesn't throw if the predicate doesn't throw |
| list::unique() | 244 | Doesn't throw if comparing the elements doesn't throw |
| list::splice() | 245 | Doesn't throw |
| list::merge() | 246 | Either succeeds or has no effect if comparing the elements doesn't throw |
| list::reverse() | 246 | Doesn't throw |
| list::swap() | 237 | Doesn't throw |
| [multi]set::insert() | 240 | For single elements either succeeds or has no effect |
| [multi]set::erase() | 242 | Doesn't throw |
| [multi]set::clear() | 244 | Doesn't throw |
| [multi]set::swap() | 237 | Doesn't throw if copying/assigning the comparison criterion doesn't throw |
| [multi]map::insert() | 240 | For single elements either succeeds or has no effect |
| [multi]map::erase() | 242 | Doesn't throw |
| [multi]map::clear() | 244 | Doesn't throw |
| [multi]map::swap() | 237 | Doesn't throw if copying/assigning the comparison criterion doesn't throw |
[1] Historically, container adapters are part of the STL. However, from a conceptional perspective, they are not part of the STL framework; they "only" use the STL.
[2] If a system does not provide member templates, it will typically allow only the same types. In this case, you can use the copy() algorithm instead. See page 188 for an example.
[3] Thanks to John H. Spicer from EDG for this explanation.
[4] In the original STL, the header file for vectors was <vector.h>.
[5] In systems without support for default template parameters, the second argument is typically missing.
[6] You (or your compiler) might consider this statement as being incorrect because it calls a nonconstant member function for a temporary value. However, standard C++ allows you to call a nonconstant member function for temporary values.
[7] reserve() manipulates the vector because it invalidates references, pointers, and iterators to elements. However, it is mentioned here because it does not manipulate the logical contents of the container.
[8] A proxy allows you to keep control where usually no control is provided. This is often used to get more security. In this case, it maintains control to allow certain operations, although the return value in principle behaves as bool.
[9] In the original STL, the header file for deques was <deque.h>.
[10] In systems without support for default template parameters, the second argument is typically missing.
[11] In the original STL, the header file for lists was <list.h>.
[12] In systems without support for default template parameters, the second argument is typically missing.
[13] The remove_if() member function is usually not provided in systems that do not support member templates.
[14] In the original STL, the header file for sets was <set.h>, and for multisets it was <multiset.h>.
[15] In systems without support for default template parameters, the second argument typically is mandatory.
[16] In systems without support for default template parameters, the third argument typically is missing.
[17] In fact, sets and multisets are typically implemented as "red-black trees." Red-black trees are good for both changing the number of elements and searching for elements. They guarantee at most two internal relinks on insertions and that the longest path is at least twice as long as the shortest path to an element.
[18] Note that you have to put a space between the two ">" characters. ">>" would be parsed as shift operator, which would result in a syntax error.
[19] In systems without support for default template parameters, you typically must always pass the sorting criterion as follows:
[20] The definition of distance() has changed, so in older STL versions you must include the file distance.hpp, which is mentioned on page 263.
[21] This statement requires several new language features; namely, member templates and default template arguments. If your system does not provide them, you must program as follows:
[22] In the original STL, the header file for maps was <map.h>, and for multimaps it was <multimap.h>.
[23] In systems without support for default template parameters, the third argument typically is mandatory.
[24] In systems without support for default template parameters, the fourth argument typically is missing.
[25] Note that you have to put a space between the two ">" characters. ">>" would be parsed as shift operator, which would result in a syntax error.
[26] In systems without support for default template parameters, you typically must always pass the sorting criterion as follows:
[27] pos->first is a shortcut for (*pos).first. Some old libraries might only provide the latter.
[28] If your system does not provide member templates, you must pass an element with the correct type. This usually requires that you make the type conversions explicit.
[29] In German all nouns are written with an initial capital letter whereas all verbs are written in lowercase letters.
[30] I first heard of the Open Closed Principle from Robert C. Martin, who himself heard it from Bertrand Meyer.
[31] Instead of invasive and noninvasive sometime the terms intrusive and nonintrusive are used.
[32] The original array wrapper class by Bjarne Stroustrup is called c_array and is defined in Section 17.5.4 of his book. I have modified it slightly for this book.
[33] Many thanks to Greg Colvin and Beman Dawes for feedback on implementing this class.
[34] The second version of unique() is available only in systems that support member templates (see page 11).
[35] The second form of sort() is available only in systems that support member templates (see page 11).
[36] The second form of merge() is available only in systems that support member templates (see page 11).
[37] Many thanks to Greg Colvin and Dave Abrahams for providing this table.
| CONTENTS |
| Browser Based Help. Published by chm2web software. |